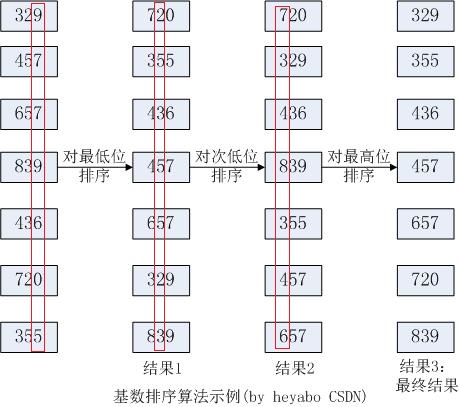
快速排序被广泛认为它是解决一般问题的最佳排序算法,它比较适合解决大规模数据的排序。
原理思想:(从小到大)
快速排序首先选取一个“基准数”,通过基准数将大于它和小于它的数无序地放在基准数的两边
什么叫无序?就是大于基准数的所有数只需要放在它的右边,这些数之间不被要求为有序,同样,小于基准数的数所有只需要放在它的左边,不被要求有序
这样就利用“基准数”对整个原始数列进行了分割成两部分,然后通过递归,用上述同样的方法选取一个基准数进行分割,直至整个数列被分割的各部分已不能再被分割
下面进行演示,基准数用定义一个变量 pivot 存放,每一部分的分割开始都是选择low下标对应的数
这里演示的就是代码中 partition函数 的实现
开始:(假设low=0,high=6. 当前的low是红色,high是绿色,pivot是蓝色,被放置好在基准数两边的数用蓝色字体表示)
原始数列a[7]
0 1 2 3 4 5 6
5 4 7 9 2 1 3
首先,选取基准数进行分割,选择low下标当前的元素5为基准数,即pivot = 5
然后将 pivot 与 high 下标对应的数进行对比
如果 <= a[high],则 low++
如果 > a[high] ,则交换 a[low] 与 a[high]
结果如下:
第一次
0 1 2 3 4 5 6
3 4 7 9 2 1 5 从上图可以看出,a[low] 与 a[high]已被交换
注意!
在这个时候,因 pivot = 5 被交换到 high 的下标处
那么接下来的比较就是将pivot与low下标当前的数进行对比
如果 >= a[low],则 low++
如果 < a[low] ,则交换 a[low] 与 a[high]
这里是比low对应的数大,结果如下:
第二次
0 1 2 3 4 5 6
3 4 7 9 2 1 5
继续使用pivot = 5 与 a[low] 进行对比
结果如下:
第三次
0 1 2 3 4 5 6
3 4 7 9 2 1 5
继续使用 pivot = 5 与 a[low] 进行对比
这时候 pivot = 5比 a[low] 小,所以又进行a[low] 与 a[high]交换
结果如下:
第四次
0 1 2 3 4 5 6
3 4 5 9 2 1 7
注意!
在这个时候,因pivot = 5被交换到low的下标处
那么接下来的比较就是将pivot与high下标当前的数进行对比
如果 >= a[high],则 high--
如果 < a[high] ,则交换 a[low] 与 a[high]
结果如下:
第五次
0 1 2 3 4 5 6
3 4 5 9 2 1 7继续使用 pivot = 5 与 a[high] 进行对比
同样进行交换,结果如下:
第六次
0 1 2 3 4 5 6
3 4 1 9 2 5 7继续使用 pivot = 5 与 a[low] 进行对比
结果如下:(low++)
第七次
0 1 2 3 4 5 6
3 4 1 9 2 5 7继续使用 pivot = 5 与 a[low] 进行对比
结果如下:
第八次
0 1 2 3 4 5 6
3 4 1 5 2 9 7继续使用 pivot = 5 与 a[high] 进行对比
结果如下:(high--)
第九次
0 1 2 3 4 5 6
3 4 1 5 2 9 7继续使用 pivot = 5 与 a[high] 进行对比
结果如下:(最终结果low == high,橙色表示)
第九次
0 1 2 3 4 5 6
3 4 1 2 5 9 7最后由于 low++ 所以 low == high
到这里,已经利用 基准数pivot = 5 把这个数列分为了两部分(5 的左边都是小于它的,右边都是大于它的)
然后递归。用同样的方法,对分割出来的两部分用“基准数”继续进行分割
快排函数代码:
[cpp]
//快排函数
void sort(int *s, int low, int high)
{
int pivot;
//if语句的判断是结束递归的简单情景,不能缺
if (low < high)
{
// partition 函数就是利用基准数进行分割的功能函数,这个函数是重点
pivot = partition(s, low, high);
sort(s, pivot + 1, high);
sort(s, low, pivot - 1);
}
}
什么是递归的简单情景?可以看看这里
partition 函数代码:
[cpp]
//这个函数就是上面演示的代码实现
int partition(int *s, int low, int high)
{
int pivot;
pivot = s[low];
while (low < high)
{
while (low < high && pivot <= s[high])
{
high--;
} www.zzzyk.com
swap(&s[low], &s[high]);
while (low < high && pivot >= s[low])
{
low++;
}
swap(&s[high], &s[low]);
}
return low;
}