UVa 10827 - Maximum sum on a torus

原题：
A grid that wraps both horizontally and vertically is called a torus. Given a torus where each cell contains an integer, determine the sub-rectangle with the largest sum. The sum of a sub-rectangle is the sum of all the elements in that rectangle. The grid below shows a torus where the maximum sub-rectangle has been shaded.

1
-1
0
0
-4
2
3
-2
-3
2
4
1
-1
5
0
3
-2
1
-3
2
-3
2
4
1
-4
Input
The first line in the input contains the number of test cases (at most 18). Each case starts with an integer N (1≤N≤75) specifying the size of the torus (always square). Then follows N lines describing the torus, each line containing N integers between -100 and 100, inclusive.

Output
For each test case, output a line containing a single integer: the maximum sum of a sub-rectangle within the torus.

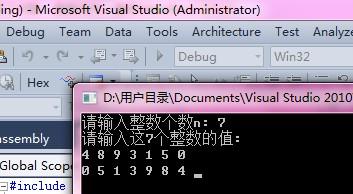
样例输入：
2
5
1 -1 0 0 -4
2 3 -2 -3 2
4 1 -1 5 0
3 -2 1 -3 2
-3 2 4 1 -4
3
1 2 3
4 5 6
7 8 9

样例输出：
15
45

思路与总结：
是上一题（UVa 108 - Maximum Sum）的再次升级版。情况变复杂了很多。这个矩阵是可以“循环转动”的。例如，当所有行都上升一行，那么第一行就会变成最后一行（原先第2行变成第1行，第3行变成第2行……），当所有行下降一行，最后一行就变成第一行。同理，列也是循环的，把上一句话的所有“行“字变成”列“字就是列循环的情况。
怎样处理这种情况呢？
如果之前做过什么涉及到圆环啊之类的题目，那么肯定马上会想到把在原数组后面再增加重复一遍这个数列的数。例如1，2，3，4，处理后变成1，2，3，4，1，2，3。那么这个新序列就可以枚举圆环出所有的连续序列。
同理，这题需要扩大增加这个矩阵，把这个存这个矩阵数字的数组的每一行增加一倍，重复一遍数字，每一列也增加一倍重复一遍。最后形成一个新的2N*2N的大矩阵。

然后再在这个新的大矩阵中找到尺寸小于等于N*N的子矩阵的最大和。
由于增加了一个限制：子矩阵的尺寸要小于等于N*N，那么在进行求“最大连续和”的过程时，要进行线性扫描，这里需要用到单调队列的应用（以前做过一道单调队列求最大连续和长度有限制的题：Max Sum of Max-K-sub-sequence)。单调队列的用处就是维护一个长度小于N的最小值。

代码：
[cpp]
/*
* UVa: 10827 - Maximum sum on a torus
* Time: 0.236s
* Author: D_Double
*/
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define MAXN 250
using namespace std;

struct Node{
    int val; // 值
    int no; // 下标
};

int arr[MAXN][MAXN], sum[MAXN][MAXN], N, ans;

inline void input(){
    memset(arr, 0, sizeof(arr));
    memset(sum, 0, sizeof(sum));
    for(int i=1; i<=N; ++i){
        for(int j=1; j<=N; ++j)
            scanf("%d", &arr[i][j]);
        for(int j=N+1; j<2*N; ++j)
            arr[i][j]=arr[i][j-N];
    }
    for(int i=N+1; i<2*N; ++i){
        for(int j=1; j<2*N; ++j)
            arr[i][j] = arr[i-N][j];
    }
    // 转化
    for(int i=1; i<2*N; ++i){
        for(int j=1; j<2*N; ++j)
            sum[i][j] = arr[i][j]+sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1];
    }
}

inline void solve(){
    deque<Node>que;
    Node temp;
    int maxSum=-2147483646;

    for(int i=1; i<2*N; ++i){
        for(int j=(i-N>=0?i-N:0) ; j<i; ++j){ // 枚举
            que.clear(); // 记住要清空！！
            int prev=0;
            for(int k=1; k<2*N; ++k){
                // 维护单调队列
                while(!que.empty() && que.back().val > prev)
                    que.pop_back();
                while(!que.empty() && que.front().no < k-N)
                    que.pop_front();
                temp.val=prev, temp.no=k-1;
                que.push_back(temp);

                int val=sum[i][k]-sum[j][k]-que.front().val;

                if(val>maxSum) maxSum=val;
                prev = sum[i][k]-sum[j][k];
            }
        }
    }
    printf("%d\n", maxSum);
}

int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        scanf("%d",&N);
        input();
        solve();
    }
}
作者：shuangde800

补充：软件开发 , C++ ,