java RSA加密解密算法入门

一、入门闲话
    最近在学javase，想拿个小题目练习。拿到一个关于socket接口实现基于TCP协议的通信(准确的说是多进程程序中通信问题。)。通信过程中需要用RSA算法进行加解密。
要求进程应用软件A 键盘输入数据后和第一端口号-1存入一SendDate对象sd1中，然后将sd1进行序列化后，将序列化后的数据进行RSA加密（此处的RSA加密用最终接收方D的公钥加密）。将第一次RSA加密后的数据和第二端口号P2，存入第二SendDate对象sd2中，接着再将sd2进行序列化，再将sd2 序列化后的数据进行RSA加密（用中间中转进程应用软件C的公钥加密）和第三端口号P3，存入到第三SendDate对象sd3中。将sd3序列化，并用用中间中转进程应用软件B的公钥加密。然后起始的应用软件A将加密后的sd3，用端口号 P0发送到B中。
   B在接到后，用B的私钥进行解密，能自动获取到下个发送的端口号P3，将数据发给用中间中转进程应用软件C，C用自己的私钥进行解密后，可获取下个端口号P2。将解密的数据发给最终的D。这样D用自己的私钥进行解密后，即可猎取A发送给来的原文了。
   题目的整体思路是清晰的，如图：

但悲剧的时，对RSA加密与解密一无所知。郁闷，只好去查相关的资料。于是有了此遍博文。
二、正题，RSA简介及深入浅出的剖析原理：
      RSA是第一个比较完善的公开密钥算法，它既能用于加密，也能用于数字签名。RSA以它的三个发明者Ron Rivest, Adi Shamir, Leonard Adleman的名字首字母命名，这个算法经受住了多年深入的密码分析，虽然密码分析者既不能证明也不能否定RSA的安全性，但这恰恰说明该算法有一定的可信性，目前它已经成为最流行的公开密钥算法。
     RSA的安全基于大数分解的难度。其公钥和私钥是一对大素数（100到200位十进制数或更大）的函数。从一个公钥和密文恢复出明文的难度，等价于分解两个大素数之积（这是公认的数学难题）。
     RSA的公钥、私钥的组成，以及加密、解密的公式可见于下表：

算法描述：
（1）选择一对不同的、足够大的素数p和q。
（2）计算n=pq。
（3）计算f(n)=(p-1)(q-1)，同时对p和q严加保密，不让任何人知道。
（4）找一个与f(n)互质的数e，且1<e<f(n)。
（5）计算d，使得de mod f(n)≡1 mod f(n)。这个公式也可以表达为d≡e-1 mod f(n)
这里要解释一下，≡是数论中表示同余的符号。公式中，≡符号的左边必须和符号右边同余，也就是两边模运算结果相同。显而易见，不管f(n)取什么值，符号右边1 mod f(n)的结果都等于1；符号的左边d与e的乘积做模运算后的结果也必须等于1。这就需要计算出d的值，让这个同余等式能够成立。
（6）公钥KU=(e,n)，私钥KR=(d,n)。
（7）加密时，先将明文变换成0至n-1的一个整数M。若明文较长，可先分割成适当的组，然后再进行交换。设密文为C，则加密过程为：C≡Me (mod n)
（8）解密过程为：M≡Cd (mod n)
实例描述：
为了更好的理解这里以简单的小例子来剖析下RSA的工作原理。为了便于计算。在以下实例中只选取小数值的素数p,q,以及e，假设用户A需要将明文“key”通过RSA加密后传递给用户B，过程如下：
（1）设计公私密钥(e,n)和(d,n)。
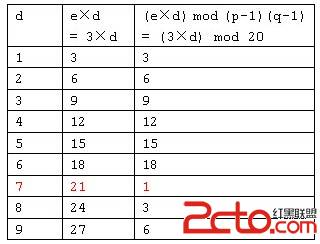
令p=3，q=11，得出n=p×q=3×11=33；f(n)=(p-1)(q-1)=2×10=20；取e=3，（3与20互质）则e×d≡1 mod f(n)，即3×d≡1 mod 20。d怎样取值呢？可以用试算的办法来寻找。试算结果见下表：

通过试算我们找到，当d=7时，e×d≡1 mod f(n)同余等式成立。因此，可令d=7。从而我们可以设计出一对公私密钥，加密密钥（公钥）为：KU =(e,n)=(3,33)，解密密钥（私钥）为：KR =(d,n)=(7,33)。
（2）英文数字化。
将明文信息数字化，并将每块两个数字分组。假定明文英文字母编码表为按字母顺序排列数值，即：

则得到分组后的key的明文信息为：11，05，25。
（3）明文加密
用户加密密钥(3,33)将数字化明文分组信息加密成密文。由C≡Me (mod n)得：

因此，得到相应的密文信息为：11，31，16。，求C1、C2..的过程
（4）密文解密。
用户B收到密文，若将其解密，只需要计算M≡Cd (mod n)，即：

用户B得到明文信息为：11，05，25。根据上面的编码表将其转换为英文，我们又得到了恢复后的原文“key”。
您看，它的原理就可以这么简单地解释！当然，实际运用要比这复杂得多，由于RSA算法的公钥私钥的长度（模长度）要到1024位甚至2048位才能保证安全，因此，p、q、e的选取、公钥私钥的生成，加密解密模指数运算都有一定的计算程序，需要仰仗计算机高速完成。
最后简单谈谈RSA的安全性。
首先，我们来探讨为什么RSA密码难于破解？在RSA密码应用中，公钥KU是被公开的，即e和n的数值可以被第三方易做图者得到。破解RSA密码的问题就是从已知的e和n的数值（n等于pq），想法求出d的数值，这样就可以得到私钥来破解密文。从上文中的公式：d ≡e-1 (mod((p-1)(q-1)))或de≡1 (mod((p-1)(q-1))) 我们可以看出。密码破解的实质问题是：从pq的数值，去求出(p-1)和(q-1)。换句话说，只要求出p和q的值，我们就能求出d的值而得到私钥。
当p和q是一个大素数的时候，从它们的积pq去分解因子p和q，这是一个公认的数学难题。比如当pq大到1024位时，迄今为止还没有人能够利用任何计算工具去完成分解因子的任务。因此，RSA从提出到现在已近二十年，经历了各种攻击的考验，逐渐为人们接受，普遍认为是目前最优秀的公钥方案之一。
然而，虽然RSA的安全性依赖于大数的因子分解，但并没有从理论上证明破译RSA的难度与大数分解难度等价。即RSA的重大缺陷是无法从理论上把握它的保密性能如何。
此外，RSA的缺点还有：A)产生密钥很麻烦，受到素数产生技术的限制，因而难以做到一次一密。B)分组长度太大，为保证安全性，n 至少也要 600 bits 以上，使运算代价很高，尤其是速度较慢，较对称密码算法慢几个数量级；且随着大数分解技术的发展，这个长度还在增加，不利于数据格式的标准化。因此，使用RSA只能加密少量数据，大量的数据加密还要靠对称密码算法。
三、Java中 RSA加解密的示例
1. 关键类的简单介绍：
   javax.crypto.Cipher   此类为加密和解密提供密码功能，还可以根据提供的byte[]数据进行加密或解密（当然前提是要提供一个密钥，公钥或私钥）
   java.security.PrivateKey
   java.security.PublicKey 公私钥对象，不用说。它们可以由KeyPair来获取
   sun.misc.BASE64Encoder
   sun.misc.BASE64Decoder 是Base64的一对加密与解码算法，这个比较简单。其实它不是主要用来加密与解密的，它主要是用来对数据进行再编码以防止某些部分数据与特殊字符有冲突，而将数据内容提升。比如它的加密过程是将数据的每6位取出后，在前两位补两个0，组成一个新的字节。最终组成新的数据byte[]。而解密过程是将数据取出后，删除去掉每个字节中的前两位同时向下个字节要两位，组成新的字节就OK了。举例如 aaaabbbb ccccdddd eeeeffff 这样的三个字节，被BASE64Encoder后，就变成了00aaaabb 00bbcccc   00ddddee 00eeffff 四个字节了。然后经BASE64Decoder解码，去掉前面两个0后就还原了。这个比较简单不作本文重点就不再细谈了。
2.上面说了一堆废话，现在给个代码示例：
2.1 Coder，BASE64进行简单的数据处理。
[java]
package com.rsa;

import java.security.MessageDigest;

import sun.misc.BASE64Decoder;
import sun.misc.BASE64Encoder;

/**
* 小加解密类，主要是BASE64的加解密
* @author chen
*
*/
public class Coder {
    public static final String KEY_SHA = "SHA";
    public static final String KEY_MD5 = "MD5";

    /**
     * BASE64解密
     *
     * @param key
     * @return
     * @throws Exception
     */
    public static byte[] decryptBASE64(String key) throws Exception {
        return (new BASE64Decoder()).decodeBuffer(key);
    }

    /**
     * BASE64加密
     *
     * @

补充：综合编程 , 安全编程 ,