POJ 1799 几何题目 题意简单明了
Yeehaa!
Time Limit: 1000MS Memory Limit: 30000K
Total Submissions: 10275 Accepted: 5181
Description
Background
George B. wants to be more than just a good American. He wants to make his daddy proud and become a western hero. You know, like John Wayne.
But sneaky as he is, he wants a special revolver that will allow him to shoot more often than just the usual six times. This way he can fool and kill the enemy easily (at least that's what he thinks).
Problem
George has kidnapped ... uh, I mean ... "invited" you and will only let you go if you help him with the math. The piece of the revolver that contains the bullets looks like this (examples for 6 and 17 bullets):
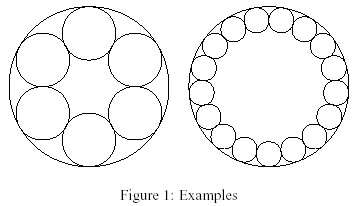
There is a large circle with radius R and n little circles with radius r that are placed inside on the border of the large circle. George wants his bullets to be as large as possible, so there should be no space between the circles. George will decide how large the whole revolver will be and how many bullets it shall contain.Your job is, given R and n, to compute r.
Input
The first line contains the number of scenarios. For each scenario follows a line containing a real number R and an integer n, with 1 <= R <= 100 and 2 <= n <= 100.
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print the value for r, rounded to three decimal places. Terminate the output for the scenario with a blank line.
Sample Input
4
4.0 6
4.0 17
3.14159 100
42 2
Sample Output
Scenario #1:
1.333
Scenario #2:
0.621
Scenario #3:
0.096
Scenario #4:
21.000
Source
TUD Programming Contest 2004, Darmstadt, Germany
题意:
给出大圆半径 以及其内的小圆个数 求小圆的半径
思路:
大圆中心A 与小圆中心B相连 之后与2小圆交点相连 得到一个垂直三角形 由此可得出关系
#include<stdio.h>
#include<math.h>
const double PI=acos(-1.0);
int main()
{
int cas,i,j=0,n;
double R,r;
scanf("%d",&cas);
while(cas--)
{
j++;
scanf("%lf %d",&R,&n);
printf("Scenario #%d:\n",j);
r=(R*sin(PI/(n*1.0)))/(1+sin(PI/(n*1.0)));
printf("%.3lf\n\n",r);
}
return 0;
}
补充:软件开发 , C++ ,