zoj3647Gao the Grid

题目意思：在一个n*m个方格中（顶点有（n+1）*(m+1)个），求所有三角形数，即三点不共线的所有情况。
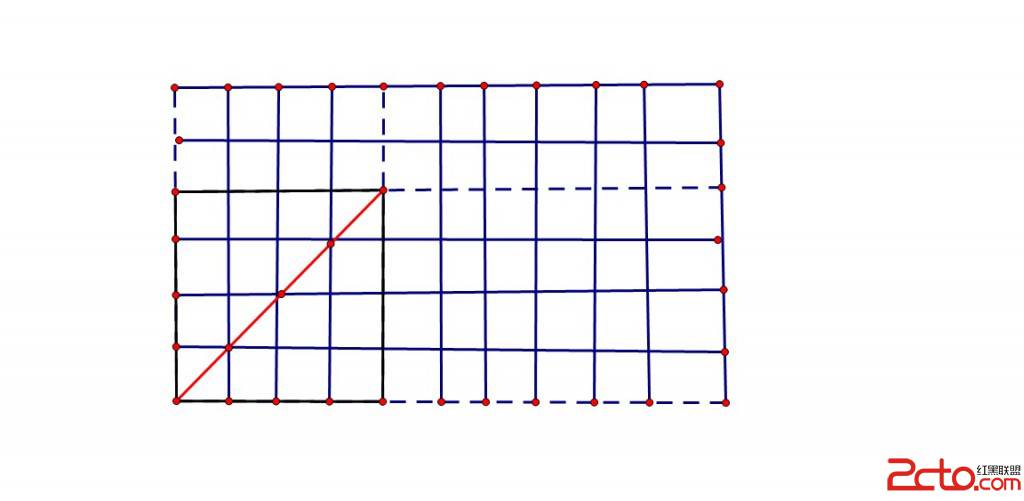
题解：令所有点的个数为t,用c[t,3]来枚举所有情况，用总数扣去所有三点共线数就是所求的三角形数。那么在求三点共线的情况时，水平和垂直的情况读者自己考虑。对于倾斜的情况，先枚举两端的端点，如图，在一个6*10的方格中选4*4的两个端点，其中可构成三点花线的另一点的个数为最大公约数易做图(4,4) -1.如图中的三个点，然后用乘于剩下的倍数（6-4+1）*（10-4+1），再乘于2（倾斜时有右上，右下两种情况）.然后依次枚举所有的矩形，求出所有三点共线的情况。于是所有情况减三点共线情况就是答案了。
 

 
 
 
代码如下：
[cpp] 
/*  
 * File:   main.cpp 
 * Author: ssslpk 
 * 
 * Created on September 29, 2012, 12:20 PM 
 */  
  
#include <cstdlib>  
#include<math.h>  
#include<stdio.h>  
#define int64 long long int  
using namespace std;  
#define N 1002  
int64 f[N][N];  
int 易做图(int a,int b){return b? 易做图(b,a%b): a;}  
void init()  
{  
    for(int i=1;i<=1000;i++)  
    {  
        for(int j=i;j<=1000;j++)  
        {  
            int d=易做图(i,j);  
            f[i][j]=f[j][i]=(int64)(d-1);  
        }  
    }  
}  
int main() {  
    int64 n,m;  
    init();  
    while(scanf("%lld%lld",&n,&m)!=EOF)  
    {  
        int64 sum=0;  
        for(int64 i=1;i<=n;i++)  
        {  www.zzzyk.com
            for(int64 j=1;j<=m;j++)  
            {  
                sum+=f[j][i]*2*(n-i+1)*(m-j+1);  
            }  
        }  
        if(n>=2)sum+=(n+1)*(n)*(n-1)/6*(m+1);  
        if(m>=2)sum+=(m+1)*(m)*(m-1)/6*(n+1);  
        int64 t=(n+1)*(m+1);  
        int64 num;  
        if(t%3==0)  
        {  
            if((t-1)%2==0)num=t/3*(t-1)/2*(t-2);  
            else num=t/3*(t-2)/2*(t-1);  
        }  
        else if((t-1)%3==0)  
        {  
            if(t%2==0)  
                num=t/2*(t-1)/3*(t-2);  
            else num=(t-1)/6*(t-2)*t;  
        }  
        else  
        {  
            if((t-1)%2==0)  
                num=(t-1)/2*(t-2)/3*t;  
            else  num=(t)/2*(t-2)/3*(t-1);  
        }  
     //   printf("sum: %lld\n",sum);  
        printf("%lld\n",num-sum);  
    }  
  
    return 0;  
}

补充：软件开发 , C++ ,