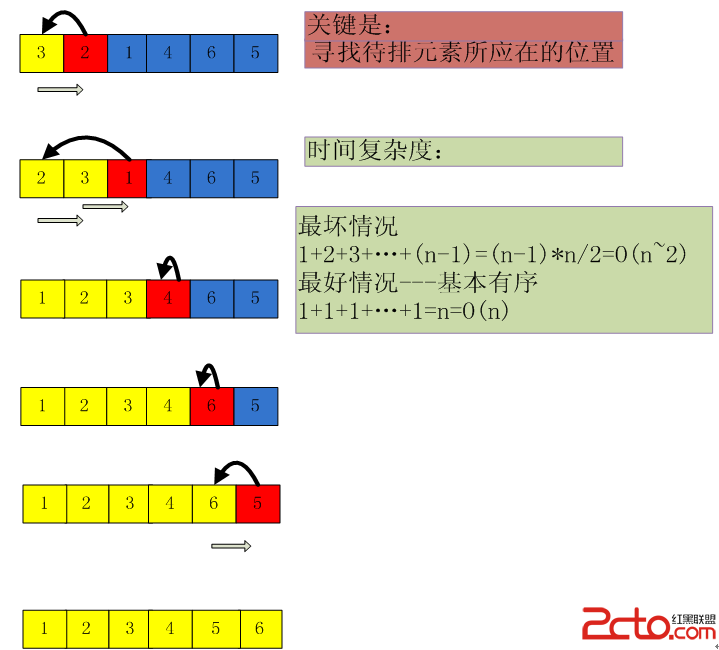
POJ 1265 pick定理

多边形边上的格点数目可以枚举每条边求出。如果是水平或者垂直，显然可以得到，否则则是坐标差的最大公约数减1.(注这里是不计算端点的，端点必然在格点上，最后统计)

 

#include <iostream>  
#include <cstdio>  
#include <cstring>  
#include <string>  
#include <algorithm>  
#include <cstdlib>  
#include <cmath>  
#include <map>  
#include <sstream>  
#include <queue>  
#include <vector>  
#define MAXN 111111  
#define MAXM 211111  
#define PI acos(-1.0)  
#define eps 1e-8  
#define INF 1000000001  
using namespace std;  
int dblcmp(double d)  
{  
    if (fabs(d) < eps) return 0;  
    return d > eps ? 1 : -1;  
}  
struct point  
{  
    double x, y;  
    point(){}  
    point(double _x, double _y):  
    x(_x), y(_y){};  
    void input()  
    {  
        scanf("%lf%lf",&x, &y);  
    }  
    double dot(point p)  
    {  
        return x * p.x + y * p.y;  
    }  
    double distance(point p)  
    {  
        return hypot(x - p.x, y - p.y);  
    }  
    point sub(point p)  
    {  
        return point(x - p.x, y - p.y);  
    }  
    double det(point p)  
    {  
        return x * p.y - y * p.x;  
    }  
    bool operator < (point a)const  
    {  
        return dblcmp(a.x - x) == 0 ? dblcmp(y - a.y) < 0 : x < a.x;  
    }  
  
}p[MAXN];  
  
int n;  
double getarea()  
{  
    double res = 0;  
    for(int i = 1; i < n; i++) res += p[i].sub(p[0]).det(p[i + 1].sub(p[0]));  
    res = fabs(res) / 2;  
    return res;  
}  
int getinedge()  
{  
    int ans = 0;  
    for(int i = 1; i <= n; i++)  
    {  
        int x = (int)fabs(p[i].x - p[i - 1].x);  
        int y = (int)fabs(p[i].y - p[i - 1].y);  
        if(x == 0 && y == 0) continue;  
        if(x == 0) ans += y - 1;  
        else if(y == 0) ans += x - 1;  
        else ans += __易做图(x, y) - 1;  
    }  
    return ans + n;  
}  
int main()  
{  
    int T;  
    double x, y;  
    int cas = 0;  
    scanf("%d", &T);  
    while(T--)  
    {  
        scanf("%d", &n);  
        p[0].x = 0, p[0].y = 0;  
        for(int i = 1; i <= n; i++)  
        {  
            scanf("%lf%lf", &x, &y);  
            p[i].x = p[i - 1].x + x;  
            p[i].y = p[i - 1].y + y;  
        }  
        double area = getarea();  
        int inedge = getinedge();  
        int inside = (int)area + 1 - inedge / 2;  
        printf("Scenario #%d:\n%d %d %.1f\n\n",++cas, inside, inedge, area);  
    }  
    return 0;  
}  

 

补充：软件开发 , C++ ,