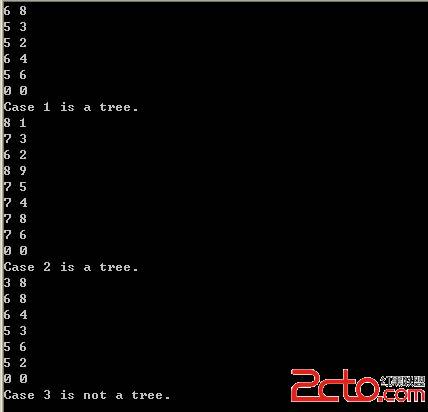
数据结构学习之二叉树(实践篇)

       上一篇博文主要对树、二叉树的概念及其一些基本特性进行简要的描述，偏向于理论知识。而本文的主要内容是针对二叉树这种数据结构的实现细节进行设计与分析，理论与实践相结合可以加深对系统知识的掌握。二叉树这种数据结构，应用非常广泛，在linux内核中随处可见，因此，如果能够熟练的掌握这项技能，将有助于理解其它系统。
        一、“初识”二叉树
        在代码的实现中，二叉树究竟是什么？请看下面代码：
[cpp]  
/*  
 * filename: bitree.h 
 * author: zhm 
 * date: 2012-01-08 
 */  
  
#ifndef BITREE_H  
#define BITREE_H  
  
#include <stdlib.h>  
  
/* define a binary tree node */  
typedef struct BiTreeNode_  
{  
    void *data;  
    struct BiTreeNode_ *left;    //point to left node.  
    struct BiTreeNode_ *right;   //point to right node.  
}BiTreeNode;  
        这是一段关于二叉树结点的数据结构，一共有3个域，数据域和左右指针域，数据域包含了二叉树每个结点的关键信息，左右指针域分别指向它的左右孩子结点。
[html]  
/* define a binary tree */  
typedef struct BiTree_  
{  
    int size;           //number of the elements in the tree.  
    BiTreeNode *root;   //root node.  
    int (*compare)(const void *key1, const void *key2);  
    void (*destroy)(void *data);  
}BiTree;  
        这里定义了一个结构体，这个结构体就是一棵二叉树了。因为它维护了一棵二叉树的重要信息，如，二叉树中结点总数size，根结点的位置root，结点数据信息的比较操作，销毁二叉树的destroy函数等。可以通过这个结构体的root域就可以方便的按深度及广度遍历整个二叉树，寻找到任何一个结点了。
        二、“深入”二叉树
        二叉树究竟是如何建立的？凡事产生均有一个过程，二叉树的建立也有一个过程。它是由不同的结点组成，按照实际情况逐一将这些结点插入从而形成二叉树，当然，也面临着结点的删除操作等，总而言之，它有以下基本操作(接口):
[cpp]  
/* public inte易做图ce */  
void bitree_init( BiTree *tree, void (*destroy)(void *data) );  
void bitree_destroy(BiTree *tree);  
int bitree_ins_left(BiTree *tree, BiTreeNode *node, const void *data);  
int bitree_ins_right(BiTree *tree, BiTreeNode *node, const void *data);  
void bitree_rem_left(BiTree *tree, BiTreeNode *node);  
void bitree_rem_right(BiTree *tree, BiTreeNode *node);  
int bitree_merge(BiTree *merge, BiTree *left, BiTree *right, const void *data);  
  
#define bitree_size(tree) ((tree)->size) //获取大小  
#define bitree_root(tree) ((tree)->root) //获取根结点  
#define bitree_is_eob(node) ((node) == NULL) //判断分支是否结束  
#define bitree_is_leaf(node) ((node)->left == NULL && (node)->right == NULL)  //判断是否是叶子结点  
#define bitree_data(node) ((node)->data) //获取数据域  
#define bitree_left(node) ((node)->left) //获取左结点(左孩子)  
#define bitree_right(node) ((node)->right)//获取右结点(右孩子)  
  
#endif  
        1 二叉树的初始化(bitree_init)：此操作完成后，一棵空的二叉树就建立了，此时它没有任何结点，这是二叉树进行后续操作的前提。
        2 二叉树的销毁(bitree_destroy)：此操作用于销毁一棵二叉树
        3 二叉树插入操作(bitree_ins_left)：将data中的信息插入到当前node结点的左指针域，成为当前node结点的左孩子。当node为NULL时，从根结点位置插入。
        4二叉树插入操作(bitree_ins_right)：同3，不同的是其插入的是右指针域。
        5 二叉树删除操作(bitree_rem_left)：删除以node结点为根的子树的左子树。当node = NULL时，则为删除整棵二叉树
        6二叉树删除操作(bitree_rem_right)：同5，不同的是其删除的是右子树。
        7 二叉树的合并(bitree_merge):将两棵二叉树，分别合并成以data域为根的新二叉树，原来这两棵二叉树分别成为新二叉树的左右子树。
        8其它宏定义：代码中已经说明清楚，这里不再累述。
        9二叉树的三种遍历操作：先序遍历、中序遍历和后序遍历。(放在后面说明)
 
        三、实现二叉树
        1、二叉树初始化的实现(bitree_init)
 
[cpp]  
/* 
 * filename: bitree.c 
 * author: zhm 
 * date: 2012-01-08 
 */  
  
#include <string.h>  
#include <stdlib.h>  
  
#include "bitree.h"  
  
/* bitree_init */  
void bitree_init( BiTree *tree, void (*destroy)(void *data) )  
{  
    /* Initialize the binary tree */  
    tree->size = 0;  
    tree->root = NULL;  
    tree->destroy = destroy;  
    return;  
}  
        完成对维护二叉树结构体的各域值的初始化。
        2、二叉树的销毁操作(bitree_destroy)
 
[cpp] 
/* bitree_destroy */  
void bitree_destroy(BiTree *tree)  
{  
    /* Remove all the nodes from the tree */  
    bitree_rem_left(tree, NULL);  
  
    memset(tree, 0, sizeof(BiTree) );  
    return;  
}  
        先删除二叉树的所有结点，然后清空二叉树结构体。
        3、二叉树插入操作(bitree_ins_left及bitree_ins_right)
 
        先是插入左子树操作：
[cpp] 
/* bitree_ins_left */  
int bitree_ins_left(BiTree *tree, BiTreeNode *node, const void *data)  
{  
    BiTreeNode *new_node, **position;  
      
    if( node == NULL )  
    {  
        if( bitree_size(tree) > 0 )  
            return -1;  
  
        position = &tree->root;  
    }  
    else  
    {  
        if( bitree_left(node) != NULL )  
            return -1;  
          
        position = &node->left;  
    }  
  
    /* Allocate storage for the node */  
    new_node = (BiTreeNode *)malloc(sizeof(BiTree

补充：软件开发 , C++ ,