几道C++试题

看到几道比较好的考察C++基础知识的试题，摘录如下。
1、下面的变量a都代表什么含义？
   （1）float(**a)[10];
    (2) double*(*a)[10];
    (3) double(*a[10])();
    (4) int*((*a)[10]);
    (5) long(*a)();
    (6) int(*(*a)(int,int))(int);

2、用变量a给出下面各项的定义。
    (1) 一个整型数
    (2) 一个指向整型数的指针
    (3) 一个指向指针的指针，它指向的指针是指向一个整型数
    (4) 一个有10个整型数的数组
    (5) 一个有10个指针的数组，该指针是指向一个整型数的
    (6) 一个指向有10个整型数数组的指针
   （7）一个指向数组的指针，该数组有10个指针，每个指针指向一个整型数
   （8）一个指向函数的指针，该函数有一个整型参数并返回一个整型数
   （9）一个有10个指针的数组，该指针指向一个函数，该函数有一个整型参数并返回一个整型数
   （10）一个指向函数的指针，该函数有一个整形参数并返回一个指向函数的指针，返回的函数指针指向有一个整型参数且返回一个整型数的函数

3、一个射击运动员打靶，靶一共有10环，连开10枪打中90环的可能性有多少种？请用递归算法编程实现。

4、输入两个整数n和m，从数列1、2、3、...n中任意取几个数，使其和等于m，要求将其中所有可能的组合都列出来，请编程求解。

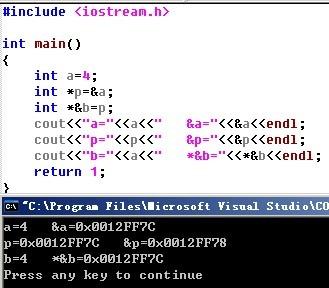
5、下面一段程序的输出是什么？
1 srand(time(NULL));
2 int nCount = 0;
3 for (int i = 0; i < LOOP_TIMES; i++)
4 {
5   int x = rand();
6   int y = rand();
7   if (x*x + y*y < RAND_MAX*RAND_MAX)
8   {
9    nCount++;
10   }
11 }
12 printf("%d\n", nCount);

6、编程将unsigned short a = 0xABCD的高低字节交换。

      这几道题考察的侧重点不一样，前两题主要考察对指针的理解，第3题和第4题都用到了递归的思想，第5题间接考察建立数学模型的能力，第6题则用到了各种位操作。下面一一进行解答。
1、 (1) a是一个二级指针，该指针指向一个一级指针，这个一级指针指向一个有10个float型元素的数组。
      (2) a是一个指针，该指针指向一个有10个指针元素的数组，每个指针元素指向一个double类型的数据。
      (3) a是一个有10个元素的数组，每个元素都是一个函数指针，该函数指针指向一个没有参数且返回double的函数。
      (4) a是一个指针，该指针指向一个有10个指针元素的数组，每个指针元素指向一个int类型的数据。
      (5) a是一个指向函数的指针，该函数没有参数且返回long。
      (6) a是一个指向函数的指针，该函数有两个整形参数并返回一个指向函数的指针，返回的函数指针指向有一个整型参数且返回一个整型数的函数。

2、 (1) int a;
      (2) int *a;
      (3) int *aa;
      (4) int a[10];
      (5) int *a[10];
      (6) int(*a)[10];
      (7) int *(*a)[10];
      (8) int(*a)(int);
      (9) int(*a[10])(int);
      (10) int(*(*a)(int))(int);

3、这道题关键是要给出递归过程中的截断条件，以下代码可作为参考。
1 #define SHOT_TIME    10
2 #define SHOT_SCORE    90
3 #define MAX_SCORE_PER_TIME   10
4
5 static int g_nCount = 0;
6 static int g_pScore[SHOT_TIME] = {0};
7
8 void Shot(int nTime, int nScore)
9 {
10 if (nScore < 0 || nScore > nTime*MAX_SCORE_PER_TIME)
11 {
12   return;
13 }
14
15 if (nTime == 1)
16 {
17   g_nCount++;
18   g_pScore[nTime-1] = nScore;
19   for (int i = 0; i < sizeof(g_pScore)/sizeof(g_pScore[0]); i++)
20   {
21    cout << g_pScore[i] << " ";
22   }
23   cout << endl;
24   return;
25 }
26
27 for (int i = 0; i <= MAX_SCORE_PER_TIME; i++)
28 {
29   g_pScore[nTime-1] = i;
30   Shot(nTime-1, nScore-i);
31 }
32 }
33
34 int main(int argc, char* argv[])
35 {
36 Shot(SHOT_TIME, SHOT_SCORE);
37 cout << "total count is " << g_n

4、这道题是一道典型的0-1背包问题，参考算法如下。
1 static bool *g_pIsSelected = NULL;
2 static int g_nNumber = 0;
3
4 void Select(int nNum, int nSum)
5 {
6 assert(g_pIsSelected != NULL);
7
8 if (nNum < 1 || nSum < 1 || (nNum==1 && nSum != 1))
9 {
10   return;
11 }
12
13 if (nNum == nSum)
14 {
15   g_pIsSelected[nNum-1] = true;
16   for (int i = 1; i <= g_nNumber; i++)
17   {
18    if (g_pIsSelected[i-1])
19    {
20     cout << i << " ";
21    }
22   }
23   g_pIsSelected[nNum-1] = false;
24   cout << endl;
25   return;
26 }
27
28 Select(nNum-1, nSum);
29
30 g_pIsSelected[nNum-1] = true;
31 Select(nNum-1, nSum-nNum);
32 g_pIsSelected[nNum-1] = false;
33 }
34
35 int main(int argc, char* argv[])
36 {
37 cout << "number is: ";
38 cin >> g_nNumber;
39 cout << "sum is: ";
40 int nSum = 0;
41 cin >> nSum;
42
43 g_pIsSelected = new bool[g_nNumber];
44 assert(g_pIsSelected != NULL);
45 memset(g_pIsSelected, 0, sizeof(bool)*g_nNumber);
46 Select(g_nNumber, nSum);
47 delete []g_pIsSelected;
48 g_pIsSelected = NULL;
49
50   cin >> nSum;
51 return 0;
52 }

5、如果仅看代码本身，是很难得到输出结果的。实际上这是一道概率题，计算的是在一个正方形内部放置一个点，点落在以正方形边长为半径的四分之一圆内的概率。由此可得输出结果为1/4*PI*1000=785（当然，在785附近的值应当都是合理的）。

6、参考代码如下。
1 int main(int argc, char* argv[])
2 {
3 unsigned short a = 0xABCD;
4 unsigned short b = a << 8;
5 unsigned short c = a >> 8;
6 a = b | c;
7 cout << hex << a << endl;
8
9 getchar();
10 return 0;
11 }

摘自创世软件团队

补充：软件开发 , C++ ,