hdu 4123 Bob’s Race(单调队列或者rmq)

 

解题思路：先求num[i]，这个如果不会的话，可以先去学下树上最长路相关知识。然后就是求这个最长区间了，由于询问是500次，且区间长度为50000，对于每次询问，考虑o(n)的算法。首先要明白的是，区间越长，那么最大值减最小值的差值就有可能越大，不可能越小（显而易见吧）。 那么我们枚举区间的右端点i，假设与i相对应的最长区间的左端点在j位置，那么对于以i+1为右端点的相应的最长区间的左端点k必然大于等于j，接下来就是怎么求这个k了。先说rmq的做法，因为rmq在询问区间最值得时候是o(1)的（这个我就不解释了），所以我们可以求[k,i]的最值（k设初值1），若不满足最值差<=q那么k++，直到满足条件（显然当k==i时，一定会满足），这样一遍扫下来，总复杂度o(n)。

 

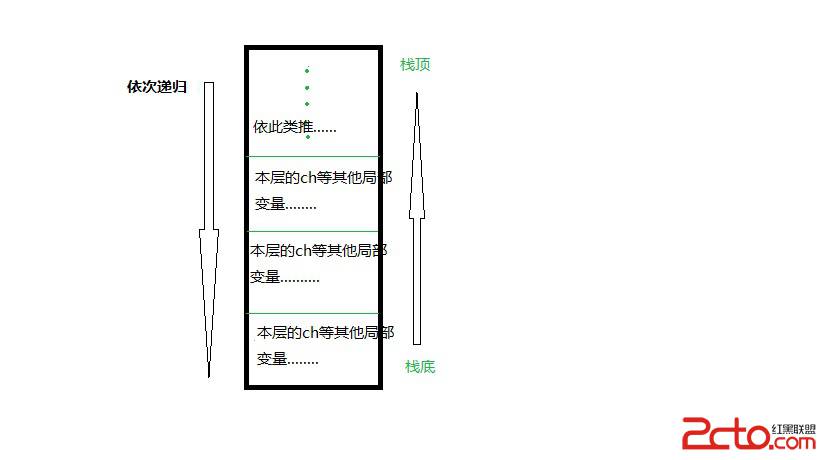
接下来讲讲单调队列的做法，我们维护两个单调队列，一个是最大值单调队列，另一个是最小值单调队列（显而易见要维护这两个嘛。。），我们还是枚举区间右端点，并且枚举到i，就把i的信息加入到单调队列（两个单调队列都加进去），然后怎么找相应的k呢（在我的代码里就是last）？取两个单调队列里的头元素（也就是最大值和最小值了），如果两者差值不符合条件，剔除pos较小的那个，直到满足为止，那么左端点k的值就是最后一次踢掉的元素的pos+1了。

 

单调队列解法代码：

 

[cpp]  

#include<stdio.h>  

#include<string.h>  

#include<algorithm>  

using namespace std ;  

  

int max ( int a , int b ) { return a > b ? a : b ; }  

int min ( int a , int b ) { return a < b ? a : b ; }  

const int maxn = 51111 ;  

int f[maxn] , n , m , num[maxn] ;  

  

struct Edge {  

    int t , next , v ;  

} edge[maxn<<1] ;  

int head[maxn] , tot ;  

  

struct Deque {  

    int val[2][maxn], pos[2][maxn];  

    int star[2] , tail[2] ;  

    void init () {  

        star[0] = 1 ;  

        tail[0] = 0 ;  

        star[1] = 1 ;  

        tail[1] = 0 ;  

    }  

    int judge (int c, int v) {  

        return c ^ (val[c][tail[c]] < v);  

    }  

    void push (int id, int v) {  

        int i ;  

        for ( i = 0 ; i < 2 ; i ++ ) {  

            while ( star[i] <= tail[i] && judge ( i , v ) )  

                tail[i] -- ;  

            val[i][++tail[i]] = v ;  

            pos[i][tail[i]] = id ;  

        }  

    }  

    void pop ( int c ) {  

        if ( star[c] <= tail[c] ) star[c] ++ ;  

    }  

    int gao ( int k , int last ) {  

        while ( val[0][star[0]] - val[1][star[1]] > k ) {  

            if ( pos[1][star[1]] < pos[0][star[0]] ) {  

                last = pos[1][star[1]] ;  

                pop ( 1 ) ;  

            }  

            else if ( pos[1][star[1]] == pos[0][star[0]] ) {  

                last = pos[1][star[1]] ;  

                pop ( 1 ) ;  

                pop ( 0 ) ;  

            }  

            else {  

                last = pos[0][star[0]] ;  

                pop ( 0 ) ;  

            }  

        }  

        return last ;  

    }  

} q ;  

  

void new_edge ( int a , int b , int c ) {  

    edge[tot].t = b ;  

    edge[tot].next = head[a] ;  

    edge[tot].v = c ;  

    head[a] = tot ++ ;  

}  

  

int mx ;  

int rt ;  

  

void dfs ( int u , int fa , int cnt ) {  

    if ( cnt >= mx ) {  

        rt = u ;  

        mx = cnt ;  

    }  

    int i ;  

    for ( i = head[u] ; i != -1 ; i = edge[i].next ) {  

        int v = edge[i].t ;  

        if ( v == fa ) continue ;  

        dfs ( v , u , cnt + edge[i].v ) ;  

    }  

}  

  

void cal ( int u , int fa , int cnt ) {  

    int i ;  

    for ( i = head[u] ; i != -1 ; i = edge[i].next ) {  

        int v = edge[i].t ;  

        if ( v == fa ) continue ;  

        num[v] = max ( num[v] , cnt + edge[i].v ) ;  

        cal ( v , u , cnt + edge[i].v ) ;  

    }  

}  

  

  

int main () {  

    int i , j ;  

    while ( scanf ( "%d%d" , &n , &m ) != EOF ) {  

        if ( n == 0 && m == 0 ) break ;  

        tot = 0 ;  

        memset ( head , -1 , sizeof ( head ) ) ;  

        memset ( num , -1 , sizeof ( num ) ) ;  

        for ( i = 1 ; i < n ; i ++ ) {  

            int a , b , c ;  

            scanf ( "%d%d%d" , &a , &b , &c ) ;  

            new_edge ( a , b , c ) ;  

            new_edge ( b , a , c ) ;  

        }  

        mx = 0 ;  

        dfs ( 1 , 0 , 0 ) ;  

        cal ( rt , 0 , 0 ) ;  

        int k = 1 ;  

        for ( i = 1 ; i <= n ; i ++ )  

            if ( num[i] > num[k] ) k = i ;  

     

补充：软件开发 , C++ ,