hdu 4044 GeoDefense （树形dp | 多叉树转二叉树）

 

题意

   这是一个塔防游戏，地图是一个n个编号为1～n的节点的树， 节点1是敌人的基地，其他叶子节点都是你的基地。

   敌人的基地会源源不断地出来怪兽，为了防止敌人攻进你的基地，你可以选择造塔。

   每个节点最多只能造一个塔，且节点i可以有ki种塔供你选择，价钱和攻击力分别为price_i, power_i

   攻击力power_i，效果是让敌人经过这个节点时让敌人的血减少power_i点。

 

   那么从敌人的基地到你的任意一个基地的路径，这条路径上的所有塔的攻击力之和，就是这个基地的抵抗力。

   敌人的攻击路径是不确定的，为了保护你的所有基地，你要确定所有基地中抵抗力最低的一个。

 

   你只有数量为m的钱，问最佳方案，可以抵挡敌人的最大血量是多少？也就是，让所有基地中抵抗力最低的一个的值尽量大，

   最大是多少？

 

思路：

 

方法一： 多叉转二叉

把多叉树先转化成“左儿子，右兄弟”的表示方法。会发现形成这样一种结构图：

 

多叉树：

 

转化成“左儿子，右兄弟”的二叉树：

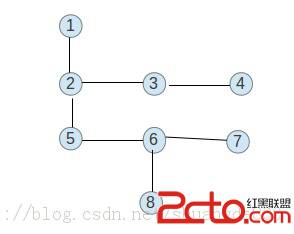
   用二叉树来思考这道题，会更自然，也更好想

   用f[i][j]表示：子树i, 用j的花费，能防守的最大HP

 

   那么, 先计算出i和它儿子一起用j的花费能防守的最大HP,

   f[i][j] = max{ f[i][j-k] + f[son][k] | 0<=k<=j}

 

   然后和它的兄弟进行状态转移：

   f[i][j] = max{ min(f[i][j-k], f[brother][k]) | 0<=k<=j} 

 

   最终f[1][m]就是答案了.

 

 

方法二：

   f[u][j]：子树u, 花j的钱的消灭的最大HP

   对于子树i, 可以选择分配k(0<=k<=j)的花费给它的所有儿子，留j-k给i点花

   对于所有的儿子要合理的分配使用这k的花费，才可以消灭的最大HP，

   用maxSon[u][k]表示所有u的所有儿子使用k的花费，可以消灭的最大HP

   我们要先求出maxSon数组, 求这个数组就和分组背包一样，因为对于每个儿子，

   可以选择分配1...k的花费给它，所以不难得到状态转移：

 

   maxSon[u][j] = max{ min(maxSon[j-k], f[v][k]) | 0<=k<=j & v是u的儿子}

 

   求出这个数组后，就可以跟新节点u的值了

   f[u][j] = max{ f[u][j-k] + maxSon[k] | 0<=k<=j }

 

小结：

上面两种方法，因为之前没做过多叉转二叉，所以一开始我想到的是方法二的，和@ZeroClock学长想的一样。而多叉转二叉是@nothi大神的提醒下知道的，然后我发现转化成二叉树来想这题更加自然，也更不容易出错。

/**=====================================================
 *   This is a solution for ACM/ICPC problem
 *
 *   @source      : hdu-4044 GeoDefense
 *   @description : 树形dp, 多叉转二叉
 *   @author      : shuangde
 *   @blog        : blog.csdn.net/shuangde800
 *   @email       : zengshuangde@gmail.com
 *   Copyright (C) 2013/08/27 13:03 All rights reserved. 
 *======================================================*/
#include <cstdio>
#include <algorithm>
#include <vector>
#include <queue>
#include <cmath>
#include <cstring>
#include <string>
#include <map>
#include <set>
#define MP make_pair
using namespace std;

typedef pair<int, int >PII;
typedef long long int64;
const double PI  = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int MAXN = 1010;

vector<int>adj[MAXN];
int n, m;
int opt[MAXN];
int price[MAXN][52], power[MAXN][52];
bool vis[MAXN];
int f[MAXN][MAXN]; 

// 左儿子，右兄弟
struct Node{
    int left, right;
}E[MAXN*2];

inline void initNode(int e) {
    E[e].left = E[e].right = -1;
}

// 多叉转二叉
void buildBinTree(int u, int fa) {
    initNode(u);
    int e, last;
    for (e = 0; e < adj[u].size(); ++e) {
        int v = adj[u][e];
        if (v == fa) continue;
        initNode(v); 
        last = E[u].left = v;
        buildBinTree(v, u);
        ++e;
        break;
    }
    for ( ; e < adj[u].size(); ++e) {
        int v = adj[u][e];
        if (v == fa) continue;
        initNode(v); 
        E[last].right = v; 
        last = v;
        buildBinTree(v, u);
    }
}

void dfs(int u) {
    for (int v = m; v >= 0; --v) {
        for (int j = 0; j < opt[u]; ++j) {
            if (price[u][j] <= v)
                f[u][v] = max(f[u][v], power[u][j]);
        }
    }
    // 和儿子的分配
    if (E[u].left !=  -1) {
        int son = E[u].left;
        dfs(son);
        for (int i = m; i >= 0; --i) {
            for (int j = 0; j <= i; ++j) 
                f[u][i] = max(f[u][i], f[u][i-j] + f[son][j]);
        }
    }

    if (E[u].right != -1) {
        int brother = E[u].right;
        dfs(brother);
        for (int i = m; i >= 0; --i) {
            int tmp = 0;
            for (int j = 0; j <= i; ++j) 
                tmp = max(tmp, min(f[u][i-j] , f[brother][j]));
            f[u][i] = tmp;
        }
    }
}

int main(){

    int nCase;
    scanf("%d", &nCase);

    while (nCase--) {
        scanf("%d", &n);

        for (int i = 0; i <= n; ++i)
            adj[i].clear();

        for (int i = 0; i < n - 1; ++i) {
            int u, v; 
            scanf("%d %d", &u, &v);
            adj[u].push_back(v);
            adj[v].push_back(u);
        }

        scanf("%d", &m);

        for (int i = 1; i <= n; ++i) {
            scanf("%d", &opt[i]);
            for (int j = 0; j < opt[i]; ++j)
                scanf("%d%d", &price[i][j], &power[i][j]);
        }

        // 多叉转二叉
        buildBinTree(1, -1);
        memset(f, 0, sizeof(f));
        dfs(1);
        printf("%d\n", f[1][m]);
    }
    return 0;
}

/**=====================================================
 *   This is a solution for ACM/ICPC problem
 *
 *   @source      : hdu-4044 GeoDefense
 *   @description : 树形dp
 *   @author      : shuangde
 *   @blog        : blog.csdn.net/shuangde800
 *   @email       : zengshuangde@gmail.com
 *   Copyright (C) 2013/08/27 13:03 All rights reserved. 
 *======================================================*/

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <queue>
#include <cmath>
#include <cstring>
#include <string>
#include <map>
#include <set>
#define MP make_pair
using namespace std;

typedef pair<int, int >PII;
typedef long long int64;
const double PI  = acos(-1.0);
const int INF = 0x3f3f3f3f;
const int MAXN = 1010;

vector<int>adj[MAXN];
int n, m;
int opt[MAXN];
int price[MAXN][52], power[MAXN][52];
int f[MAXN][MAXN]; 


// tree dp
void dfs(int u, int fa) {

    // init
    for (int v = 0; v <= m; ++v) {
        for (int j = 0; j < opt[u]; ++j) 
            if (price[u][j] <= v)
                f[u][v] = max(f[u][v], power[u][j]);
    }

    // 如果叶子节点, 退出
    if (adj[u].size()==1 && u!=1) {
        return;
    }

    // maxSon[i]: 表示所有儿子花费i时，可以消灭的最大HP
    int maxSon[210];
    memset(maxSon, INF, sizeof(maxSon));
    for (int e = 0; e < adj[u].size(); ++e) {
        int v = adj[u][e];
        if (v==fa) continue;
        dfs(v, u);
        for (int i = m; i >= 0; --i) {
            int maxx = 0;
            for (int j = 0; j <= i; ++j) {
                maxx = max(maxx, min(maxSon[i-j], f[v][j]));
            }
            maxSon[i] = maxx;
        }
    }
    for (int i = m; i >= 0; --i) {
        for (int k = 0; k <=i; ++k) {
补充：软件开发 , C++ ,