堆和堆排序

优先级队列
优先级队列是一个由相同类型的数据元素组成的集合，其中每个数据项都带有一个特定的优先级。它支持insert元素操作，findMin访问优先级最小元素的操作，deleteMin删除优先级最小元素的操作，当然，也可能是支持findMax访问优先级最大元素的操作，deleteMax删除优先级最大元素的操作，以需求而定。
有两种很自然的方法来实现优先级队列：
一种是使用无序队列（数组、向量或链表实现）。两种基本操作的实现方法及时间复杂度如下：

插入：把数据项插入到队尾或队头。时间复杂度：O(1)。
删除：遍历队列找出优先级最高或最低的项，然后删除。时间复杂度：O(n)。
另一种是使用有序队列（数组、向量或链表实现）。
两种基本操作的实现方法及时间复杂度如下：

插入：基本线性插入排序。时间复杂度：O(n)。
删除：删除队头和队尾的项。时间复杂度：O(1)。
当然，还有一个可能的实现是二叉查找树，但二叉查找树很容易变得不平衡，这样，插入和删除效率便会大大降低，另外，二叉查找树实现了比优先级队列更多的功能，可以想见，它必然也消耗了更多的资源。所以，将二叉查找树用作优先级队列的实现，实在太大材小用了。
当当当当！我们今天的主角登场了。堆，或称作二叉堆，是“已知的最优雅的数据结构之一”。堆是实现优先级队列的典型方法，两种基本操作时间复杂度如下：

插入：最坏情况下时间复杂度为O(logn)；平均情况下时间复杂度为O(1)，业已证明，执行一次插入平均需要 2.607 次比较，因此平均 insert 操作上移元素 1.607层。
删除：在平均情况和最坏情况下时间复杂度均为O(logn)。
表现简直完美！STL中的priority_queue类模板就是采用二叉堆来实现的。

堆
堆是符合下列性质的二叉树：

结构属性：堆是一棵完全树。
顺序属性：每个结点中的数据项都大于或等于儿子的数据项。
以上的顺序结构是针对最大堆而言的，最小堆的叙述则恰好相反。下面的讲解都默认为最大堆。
一般采用数组或向量来实现堆，初次接触这个事实可能会感到奇怪，因为我们所接触过的树结构都是使用链式结构来实现的。采用数组或向量来实现堆效率更高，这主要是因为堆没有在中间位置删除和插入元素的需求，另外堆是一棵完全树，方便索引。
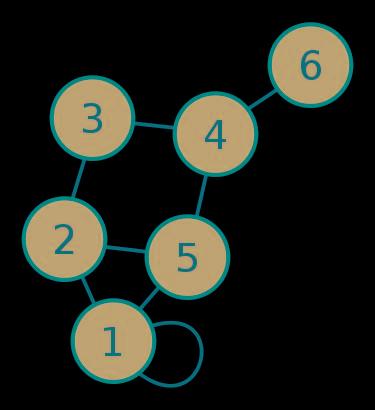
一个最大堆结构如下图所示，它既是一棵二叉树，也是一个数组。

我们来看看堆的基本操作:
1、插入操作（insert）
插入操作的过程很简单：将新数据插入到堆的下一个空位，然后向上渗透直到二叉树重新满足堆的顺序属性为止。

实现代码：

[cpp]
插入操作在平均情况下花费常量时间，在最坏情况下花费对数时间
//业已证明，执行一次插入平均需要 2.607 次比较，因此平均 insert 操作
//上移元素 1.607层。
template<typename T>
void BinaryHeap<T>::insert(const T& value)
{
    if(theSize+1==theArray.size())
        theArray.resize(theArray.size()*2);
    int hole = ++theSize;
    //hole==1时已是最高点，不可向上渗透了。
    for(;value<theArray[hole/2]&&hole>1;hole/=2)
        theArray[hole] = theArray[hole/2];
    theArray[hole] = value;
}

//插入操作在平均情况下花费常量时间，在最坏情况下花费对数时间
//业已证明，执行一次插入平均需要 2.607 次比较，因此平均 insert 操作
//上移元素 1.607层。
template<typename T>
void BinaryHeap<T>::insert(const T& value)
{
    if(theSize+1==theArray.size())
        theArray.resize(theArray.size()*2);
    int hole = ++theSize;
    //hole==1时已是最高点，不可向上渗透了。
    for(;value<theArray[hole/2]&&hole>1;hole/=2)
        theArray[hole] = theArray[hole/2];
    theArray[hole] = value;
}
2、下滤操作（percolate down）
近似堆的定义是，二叉树根结点的左右子树均为堆，但整体不满足堆的顺序属性。下滤操作是把近似堆调整为堆的过程。
该过程也很简单：找到一个较大的儿子，如果该结点比儿子小，则和儿子交换位置。重复上述过程直到二叉树满足堆的顺序属性。
下图展示了对结点2进行下滤操作的过程。

实现代码：

[cpp]
template<typename T>
void BinaryHeap<T>::percolateDown(int hole)
{
    int child;
    T temp = theArray[hole];
    for (;hole*2<=theSize;hole=child)
    {
        child = hole*2;
        if(child!=theSize && theArray[child+1]<theArray[child])
            ++child;
        if(theArray[child]<temp)
            theArray[hole]=theArray[child];
        else
            break;
    }
    theArray[hole]=temp;
}

template<typename T>
void BinaryHeap<T>::percolateDown(int hole)
{
    int child;
    T temp = theArray[hole];
    for (;hole*2<=theSize;hole=child)
    {
        child = hole*2;
        if(child!=theSize && theArray[child+1]<theArray[child])
            ++child;
        if(theArray[child]<temp)
            theArray[hole]=theArray[child];
        else
            break;
    }
    theArray[hole]=temp;
}我并没有单独列出删除操作（delete），这是因为删除操作主要过程就是下滤操作：删除根结点，将堆最后面的数据项复制到根结点，执行下滤操作。
实现代码：

[cpp]
删除操作在平均情况和最坏情况下都需要对数时间
template<typename T>
void BinaryHeap<T>::deleteMin()
{
    if(isEmpty())
        throw exception();
    theArray[1]=theArray[theSize--];
    percolateDown(1);
}

//删除操作在平均情况和最坏情况下都需要对数时间
template<typename T>
void BinaryHeap<T>::deleteMin()
{
    if(isEmpty())
        throw exception();
    theArray[1]=theArray[theSize--];
    percolateDown(1);
}
3、建堆操作（build heap）
建堆操作是把一棵完全二叉树转换成堆。这是堆排序中的关键操作。该操作的具体过程为：从最后一个非叶子节点开始到根结点，依次执行下滤操作。
下图展示了构建一个最大堆的过程。

实现代码：

[cpp]
template<typename T>
void BinaryHeap<T>::buildHeap()
{
for(int i=theSize/2;i>0;--i)
percolateDown(i);
}

template<typename T>
void BinaryHeap<T>::buildHeap()
{
for(int i=theSize/2;i>0;--i)
percolateDown(i);
}
点击此处查看最小堆类模板完整源代码

堆排序
顾名思义，堆排序是利用堆的特性来对一组数据进行排序。堆排序可分为以下个步骤（从小到大排序）：

对所有n个数据进行建堆（最大堆）操

补充：软件开发 , C++ ,