POJ 1986 Distance Queries LCA和RMQ

这题以前用tanjan做过

现在再做一遍用RMQ的方法。

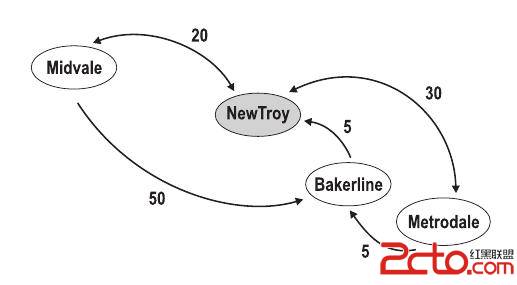
大意就是求一棵树上任意两点的距离

先DFS跑出欧拉序列

然后根据pos直接RMQ就行了

[cpp]
#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
#include <queue>
#include <map>
#include <set>
#define eps 1e-5
#define MAXN 55555
#define MAXM 111111
#define INF 1000000000
using namespace std;
int n, m, q;
struct EDGE
{
    int v, next, w;
}edge[MAXM];
int head[MAXN], e;
int index, tmpdfn;
int f[2 * MAXN], id[MAXN], vis[MAXN], pos[MAXN], dis[MAXN];
int mi[2 * MAXN][18];
void init()
{
    memset(head, -1, sizeof(head));
    e = 0;
    index = tmpdfn = 0;
    memset(vis, 0, sizeof(vis));
    dis[1] = 0;
}
void add(int u, int v, int w)
{
    edge[e].v = v;
    edge[e].w = w;
    edge[e].next = head[u];
    head[u] = e++;
}
void dfs(int u)
{
    vis[u] = 1;
    int tmp = ++tmpdfn;
    f[++index] = tmp;
    id[tmp] = u;
    pos[u] = index;
    for(int i = head[u]; i != -1; i = edge[i].next)
    {
        int v = edge[i].v;
        if(!vis[v])
        {
            dis[v] = dis[u] + edge[i].w;
            dfs(v);
            f[++index] = tmp;
        }
    }
}
void rmqinit(int n, int *w)
{
    for(int i = 1; i <= n; i++) mi[i][0] = w[i];
    int m = (int)(log(n * 1.0) / log(2.0));
    for(int i = 1; i <= m; i++)
        for(int j = 1; j <= n; j++)
        {
            mi[j][i] = mi[j][i - 1];
            if(j + (1 << (i - 1)) <= n) mi[j][i] = min(mi[j][i], mi[j + (1 << (i - 1))][i - 1]);
        }
}
int rmqmin(int l,int r)
{
    int m = (int)(log((r - l + 1) * 1.0) / log(2.0));
    return min(mi[l][m] , mi[r - (1 << m) + 1][m]);
}
int LCA(int l, int r)
{
    if(pos[l] > pos[r]) swap(l, r);
    int ans = rmqmin(pos[l], pos[r]);
    return id[ans];
}
int main()
{
    scanf("%d%d", &n, &m);
    int u, v, w, l, r;
    init();
    while(m--)
    {
        scanf("%d%d%d%*s", &u, &v, &w);
        add(u, v, w);
        add(v, u, w);
    }
    dfs(1);
    rmqinit(index, f);
    scanf("%d", &q);
    while(q--)
    {
        scanf("%d%d", &l, &r);
        printf("%d\n", dis[l] + dis[r] - 2 * dis[LCA(l, r)]);
    }
    return 0;
}

#include <iostream>
#include <algorithm>
#include <cstring>
#include <string>
#include <cstdio>
#include <cmath>
#include <queue>
#include <map>
#include <set>
#define eps 1e-5
#define MAXN 55555
#define MAXM 111111
#define INF 1000000000
using namespace std;
int n, m, q;
struct EDGE
{
    int v, next, w;
}edge[MAXM];
int head[MAXN], e;
int index, tmpdfn;
int f[2 * MAXN], id[MAXN], vis[MAXN], pos[MAXN], dis[MAXN];
int mi[2 * MAXN][18];
void init()
{
    memset(head, -1, sizeof(head));
    e = 0;
    index = tmpdfn = 0;
    memset(vis, 0, sizeof(vis));
    dis[1] = 0;
}
void add(int u, int v, int w)
{
    edge[e].v = v;
    edge[e].w = w;
    edge[e].next = head[u];
    head[u] = e++;
}
void dfs(int u)
{
    vis[u] = 1;
    int tmp = ++tmpdfn;
    f[++index] = tmp;
    id[tmp] = u;
    pos[u] = index;
    for(int i = head[u]; i != -1; i = edge[i].next)
    {
        int v = edge[i].v;
        if(!vis[v])
        {
            dis[v] = dis[u] + edge[i].w;
            dfs(v);
            f[++index] = tmp;
        }
    }
}
void rmqinit(int n, int *w)
{
    for(int i = 1; i <= n; i++) mi[i][0] = w[i];
    int m = (int)(log(n * 1.0) / log(2.0));
    for(int i = 1; i <= m; i++)
        for(int j = 1; j <= n; j++)
        {
            mi[j][i] = mi[j][i - 1];
            if(j + (1 << (i - 1)) <= n) mi[j][i] = min(mi[j][i], mi[j + (1 << (i - 1))][i - 1]);
        }
}
int rmqmin(int l,int r)
{
    int m = (int)(log((r - l + 1) * 1.0) / log(2.0));
    return min(mi[l][m] , mi[r - (1 << m) + 1][m]);
}
int LCA(int l, int r)
{
    if(pos[l] > pos[r]) swap(l, r);
    int ans = rmqmin(pos[l], pos[r]);
    return id[ans

补充：软件开发 , C++ ,