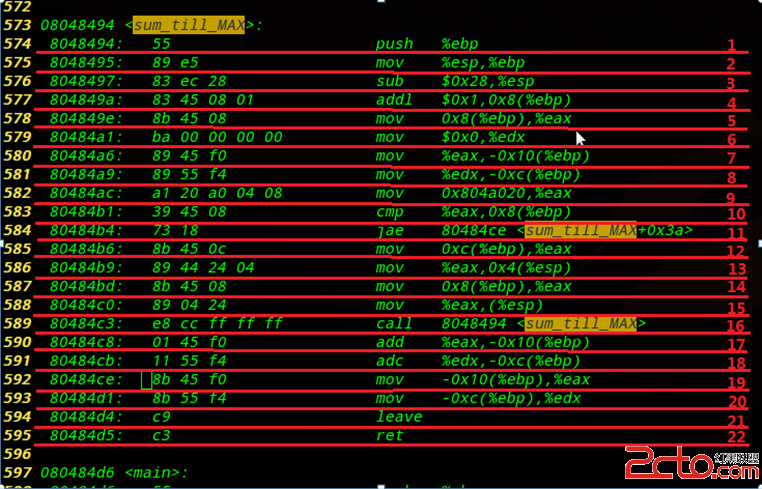
hdu4587 TWO NODES

问一个无向图中去掉任意两点后剩下的连通分量的个数最大值

枚举第一个删去的点，在剩下的子图中求割点

注意，剩下的子图可能不连通，那么就要对每个连通块求割点

计算删去一个点后剩余连通分量个数 left 的方法为：tarjan算法中的时间戳数组dfn[]若为0说明是新的连通分量

求删去割点后剩余连通分量个数：

tarjan算法中将判断是否为割点的bool 数组改为int类型，并将iscut[i] = 1 改为 iscut[i]++ 即可

那么对于非根节点，删去后剩余个数为iscut[i] + 1(子树个数加上父节点)，根节点为iscut[i] (没有父节点)

那么全题答案便是 max(iscut[i] + 1) + left - 1

细节见代码

#pragma comment(linker, "/STACK:102400000000,102400000000")  
#include <cstdio>  
#include <ctime>  
#include <cstdlib>  
#include <cstring>  
#include <queue>  
#include <string>  
#include <set>  
#include <stack>  
#include <map>  
#include <cmath>  
#include <vector>  
#include <iostream>  
#include <algorithm>  
#include <bitset>  
using namespace std;  
//LOOP  
#define FD(i, b, a) for(int i = (b) - 1; i >= (a); --i)  
#define FE(i, a, b) for(int i = (a); i <= (b); ++i)  
#define FED(i, b, a) for(int i = (b); i>= (a); --i)  
#define REP(i, N) for(int i = 0; i < (N); ++i)  
#define CLR(A,value) memset(A,value,sizeof(A))  
//OTHER  
#define PB push_back  
//INPUT  
#define RI(n) scanf("%d", &n)  
#define RII(n, m) scanf("%d%d", &n, &m)  
#define RIII(n, m, k) scanf("%d%d%d", &n, &m, &k)  
#define RIV(n, m, k, p) scanf("%d%d%d%d", &n, &m, &k, &p)  
#define RS(s) scanf("%s", s)  
typedef long long LL;  
typedef unsigned long long ULL;  
const int INF = 1000000000;  
const int MAXN = 5050;  
const int MOD = 1000000;  
  
vector<int> G[MAXN];  
int dfn[MAXN], low[MAXN], iscut[MAXN];         //时间戳数组，所能访问的最早祖先，删去此点后所能得到的连通分量个数  
int dfs_c, ans;  
int n, m, none;  
  
void add(int u, int v)  
{  
    G[u].push_back(v);  
    G[v].push_back(u);  
}  
  
int tarjan(int u, int fa)  
{  
    bool f = false;                           ///判断重边用  
    int lowu = dfn[u] = ++dfs_c;  
    int child = 0, sz = G[u].size();  
    REP(i, sz)  
    {  
        int v = G[u][i];  
        if (v == none) continue;             ///若为枚举的第一个删除的节点，忽略     
        if (v == fa && !f)  
        {  
            f = 1;  
            continue;  
        }  
        if (!dfn[v])  
        {  
            int lowv = tarjan(v, u);  
            lowu = min(lowu, lowv);  
            if (lowv >= dfn[u])  
                iscut[u]++;  
        }  
        else  
            lowu = min(lowu, dfn[v]);  
    }  
    if (fa < 0 && child == 1)                ///若为此连通分量的根节点且只有一个子树,那么删去后连通分量为 1  
        iscut[u] = 1;  
    low[u] = lowu;  
    return lowu;  
}  
  
void init()  
{  
    REP(i, n + 1)  
        G[i].clear();  
    ans = 0;  
}  
  
int solve(int x)  
{  
    int ret = 0;  
    none = x;  
    CLR(dfn, 0), CLR(low, 0);  
    CLR(iscut, 0);  
    dfs_c = 0;  
    int left = 0;  
    REP(i, n)  
        if (i != x && !dfn[i])  
            iscut[i]--, left++, tarjan(i, -1);           ///dfn为0 说明是根节点，先-1，后面统计时便全是iscut + 1  
    REP(i, n)  
    if (i != x)  
        ret = max(ret, iscut[i] + 1);  
    ret += left - 1;                             ///剩下连通分量加上最大iscut值  
    return ret;  
}  
  
int main()  
{  
    int x, y;  
    while (~RII(n, m))  
    {  
        init();  
        REP(i, m)  
        {  
            RII(x, y);  
            add(x, y);  
        }  
        REP(i, n)  
           ans = max(ans, solve(i));  
        printf("%d\n", ans);  
    }  
}  
/* 

5 5 
0 3 
3 4 
3 2 
1 2 
2 4 
*/

补充：软件开发 , C++ ,