机器学习实战：单变量线性回归的实现

一、算法实现

由前面的理论，我们知道了用梯度下降解决线性回归的公式：

梯度下降解决线性回归思路：

算法实现：

ComputeCost函数：

[plain]
function J = computeCost(X, y, theta)

    m = length(y); % number of training examples
    J = 0;
    predictions = X * theta;
    J = 1/(2*m)*(predictions - y)'*(predictions - y);

end

gradientDescent函数：

[plain]
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
% X is m*(n+1) matrix
% y is m*1
% theta is (n+1)*1 matrix
% alpha is a number
% num_iters is number of iterators


    m = length(y); % number of training examples
    J_history = zeros(num_iters, 1); %cost function的值的变化过程
    %预先定义了迭代的次数

    for iter = 1:num_iters

        temp1 = theta(1) - (alpha / m) * sum((X * theta - y).* X(:,1));
        temp2 = theta(2) - (alpha / m) * sum((X * theta - y).* X(:,2));
        theta(1) = temp1;
        theta(2) = temp2;
        J_history(iter) = computeCost(X, y, theta);

    end

end

二、数据可视化

我们通过算法实现能够求出函数h(x)，但是我们还需要将数据可视化：
(1)画出训练集的散点图+拟合后的直线；
(2)画出J(theta)为z轴，theta0为x轴，theta1为y轴的三维曲线；
(3)画出(2)的三维曲线的等高线图；

1.画散点图+拟合的直线

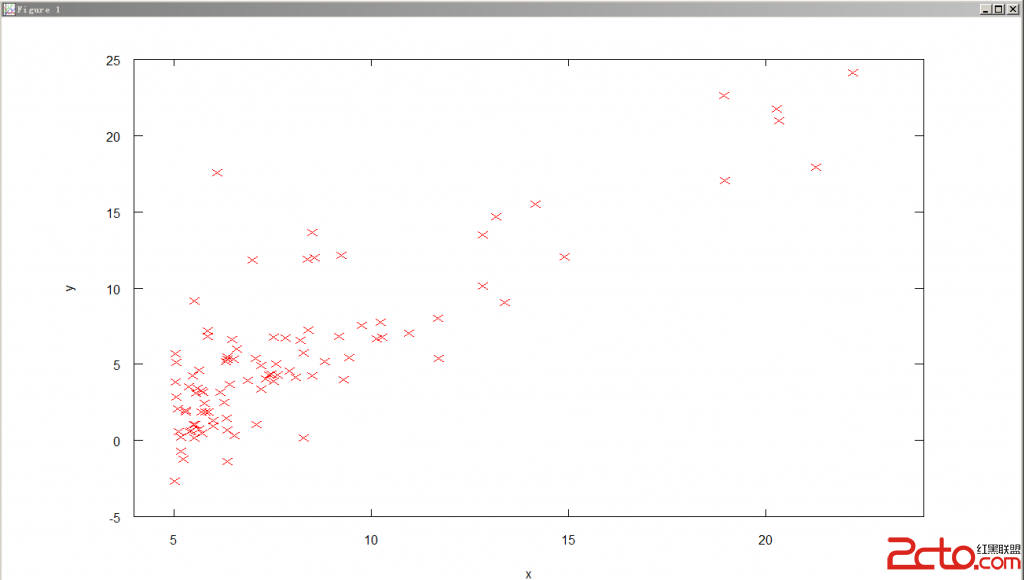
描述：给定ex1data1.txt，文件中有两列数据，每一列代表一个维度，第一列代表X，第二列代表Y，用Octave画出散布图（Scalar Plot），数据的形式如下：
6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
........

答：
(1)data = load('ex1data1.txt');             %导入该文件，并赋予data变量
(2)X = data( : , 1 )；Y = data( : , 2)；    %将两列分别赋予X和Y
(3)X = [ones(size(X,1),1),X];                  %在X的左边添加一列1
(4)plot(X,Y,'rx','MarkerSize', 4);            %画图，将X向量作为X轴，Y向量作为Y轴，每个点用“x”表示，‘r’表示红点，每个点的大小为4；
(5)axis([4 24 -5 25]);                             %调整x和y轴的起始坐标和最高坐标；
(6)xlabel('x');                                         %给x轴标号为‘x’;
(7)ylabel('y');                                        %给y轴标号为‘y’;

最后见下图：

经过计算，算出theta值：
[theta,J_history] = gradientDescent(X, y, theta, alpha, num_iters);
即可通过：
plot(X(:,2), X*theta)； %画出最后拟合的直线

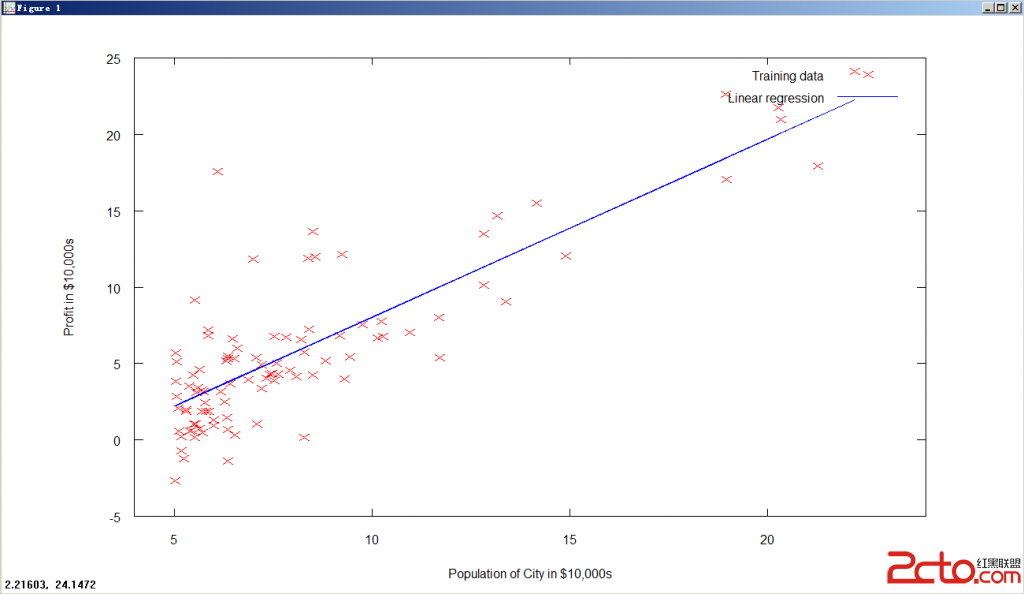
以上呈现了线性回归的结果；

以下两种都是可视化J(theta)；

2.Su易做图ce Plot

描述：数据如上一题一样，我们想要绘制出对于这些数据的cost function，我们将绘制出三维图形和contour plot；

我们如果要绘制cost function，我们必须预先写好cost function的公式：
function J = computeCost(X, y, theta)
    m = length(y);
    J = 0;
    predictions = X * theta;
    J = 1/(2*m)*sum((predictions - y) .^ 2);
end

实现：

(1)theta0_vals = linspace(-10, 10, 100);                  %从-10到10之间取100个数组成一个向量
(2)theta1_vals = linspace(-1, 4, 100);                      %从-1到4之间取100个数组成一个向量
(3)J_vals = zeros(length(theta0_vals), length(theta1_vals));   %初始化J_vals矩阵，对于某个theta0和theta1，J_vals都有对应的cost function值；
(4)计算每个（theta0，theta1）所对应的J_vals；
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
    end
end
(5)figure;                      %创建一个图
(6)surf(theta0_vals,theta1_vals,J_vals); %x轴为theta0_vals，y轴为theta1_vals，z轴为J_vals；
(7)xlabel('\theta_0');   %添加x轴标志
(8)ylabel('\theta_1');   %添加y轴标志

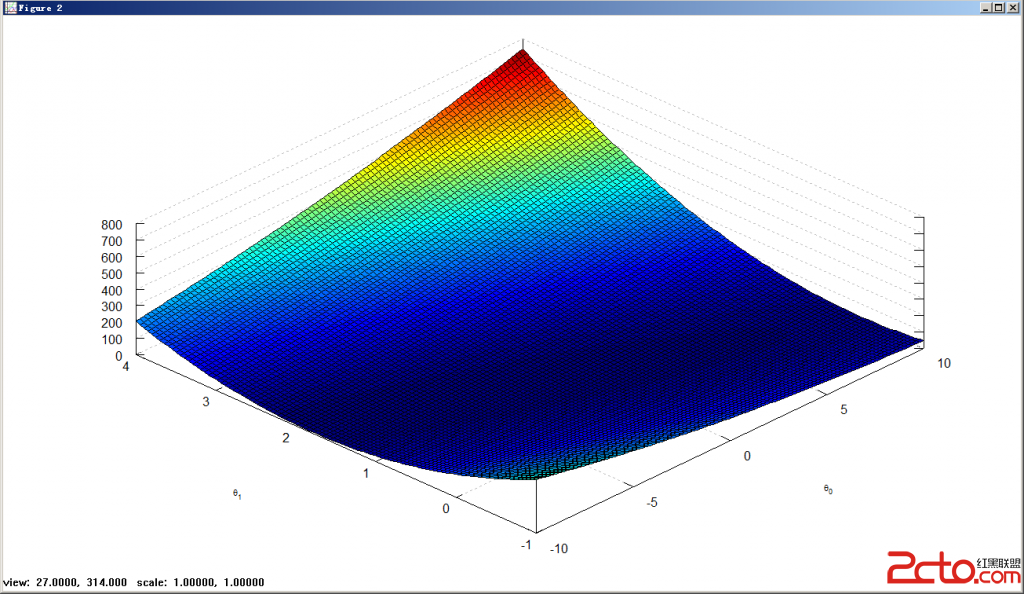
此图而且可以转动；

2.Contour Plot

实现：

(1)theta0_vals = linspace(-10, 10, 100);                  %从-10到10之间取100个数组成一个向量
(2)theta1_vals = linspace(-1, 4, 100);                      %从-1到4之间取100个数组成一个向量
(3)J_vals = zeros(length(theta0_vals), length(theta1_vals));   %初始化J_vals矩阵，对于某个theta0和theta1，J_vals都有对应的cost function值；
(4)计算每个（theta0，theta1）所对应的J_vals；
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = computeCost(X, y, t);
    end
end
(5)figure;                      %创建一个图
(6)contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20)); %画等高线图
(7)xlabel('\theta_0'); ylabel('\theta_1');

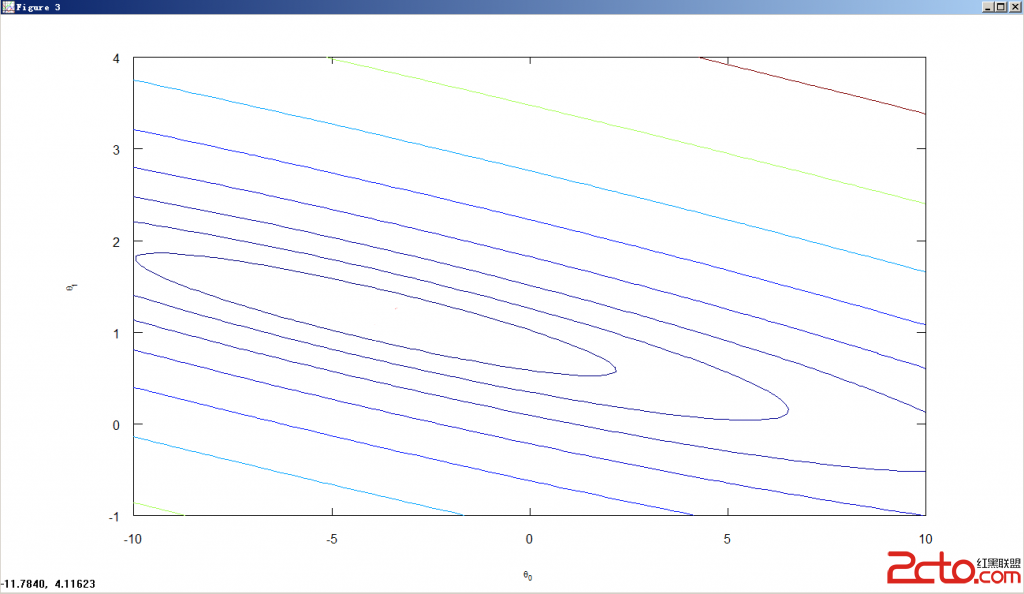
如果我们想要在等高线图上画出线性回归的theta0与theta1的结果，则可以：
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

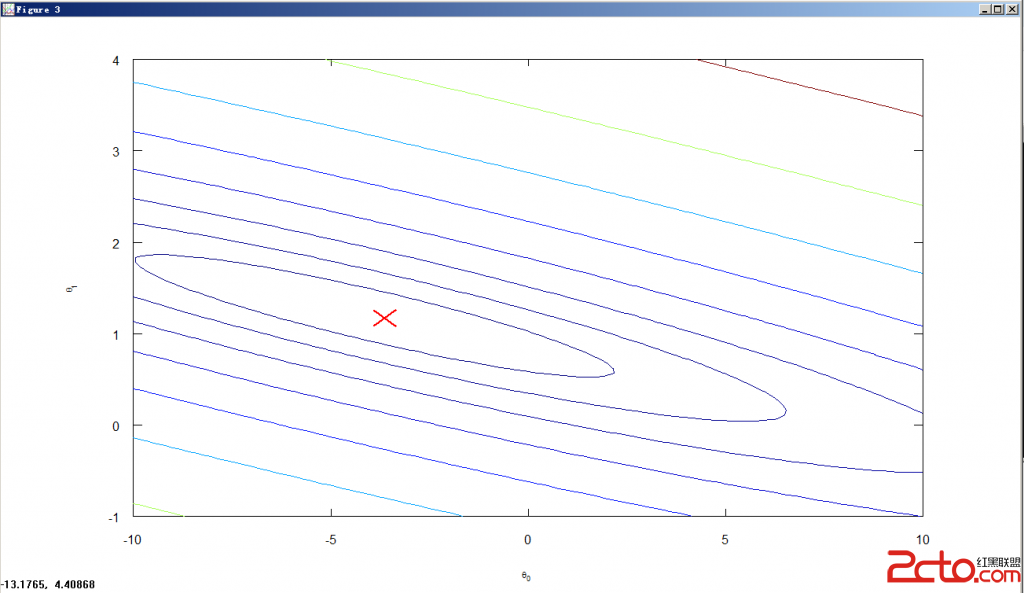
4.画图查看Learning Rate是否合理

我们在gradientDescent函数中返回的值里有J_history向量，此向量记录了每次迭代后cost function的值，因此我们只需要将x轴为迭代的次数，y轴为cost function的值，即可画图：

补充：综合编程 , 其他综合 ,