机器学习入门:线性回归及梯度下降
本文会讲到:
(1)线性回归的定义
(2)单变量线性回归
(3)cost function:评价线性回归是否拟合训练集的方法
(4)梯度下降:解决线性回归的方法之一
(5)feature scaling:加快梯度下降执行速度的方法
(6)多变量线性回归
Linear Regression
注意一句话:多变量线性回归之前必须要Feature Scaling!
方法:线性回归属于监督学习,因此方法和监督学习应该是一样的,先给定一个训练集,根据这个训练集学习出一个线性函数,然后测试这个函数训练的好不好(即此函数是否足够拟合训练集数据),挑选出最好的函数(cost function最小)即可;
注意:
(1)因为是线性回归,所以学习到的函数为线性函数,即直线函数;
(2)因为是单变量,因此只有一个x;
我们能够给出单变量线性回归的模型:
我们常称x为feature,h(x)为hypothesis;
从上面“方法”中,我们肯定有一个疑问,怎么样能够看出线性函数拟合的好不好呢?
我们需要使用到Cost Function(代价函数),代价函数越小,说明线性回归地越好(和训练集拟合地越好),当然最小就是0,即完全拟合;
举个实际的例子:
我们想要根据房子的大小,预测房子的价格,给定如下数据集:
根据以上的数据集画在图上,如下图所示:
我们需要根据这些点拟合出一条直线,使得cost Function最小;
虽然我们现在还不知道Cost Function内部到底是什么样的,但是我们的目标是:给定输入向量x,输出向量y,theta向量,输出Cost值;
以上我们对单变量线性回归的大致过程进行了描述;
Cost Function
Cost Function的用途:对假设的函数进行评价,cost function越小的函数,说明拟合训练数据拟合的越好;
下图详细说明了当cost function为黑盒的时候,cost function 的作用;
但是我们肯定想知道cost Function的内部构造是什么?因此我们下面给出公式:
其中:
表示向量x中的第i个元素;
表示向量y中的第i个元素;
表示已知的假设函数;
m为训练集的数量;
比如给定数据集(1,1)、(2,2)、(3,3)
则x = [1;2;3],y = [1;2;3] (此处的语法为Octave语言的语法,表示3*1的矩阵)
如果我们预测theta0 = 0,theta1 = 1,则h(x) = x,则cost function:
J(0,1) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0;
如果我们预测theta0 = 0,theta1 = 0.5,则h(x) = 0.5x,则cost function:
J(0,0.5) = 1/(2*3) * [(h(1)-1)^2+(h(2)-2)^2+(h(3)-3)^2] = 0.58;
如果theta0 一直为 0, 则theta1与J的函数为:

如果有theta0与theta1都不固定,则theta0、theta1、J 的函数为:

当然我们也能够用二维的图来表示,即等高线图;

注意:如果是线性回归,则costfunctionJ与的函数一定是碗状的,即只有一个最小点;
以上我们讲解了cost function 的定义、公式;
Gradient Descent(梯度下降)
但是又一个问题引出了,虽然给定一个函数,我们能够根据cost function知道这个函数拟合的好不好,但是毕竟函数有这么多,总不可能一个一个试吧?
因此我们引出了梯度下降:能够找出cost function函数的最小值;
梯度下降原理:将函数比作一座山,我们站在某个山坡上,往四周看,从哪个方向向下走一小步,能够下降的最快;
当然解决问题的方法有很多,梯度下降只是其中一个,还有一种方法叫Normal Equation;
方法:
(1)先确定向下一步的步伐大小,我们称为Learning rate;
(2)任意给定一个初始值:;
(3)确定一个向下的方向,并向下走预先规定的步伐,并更新;
(4)当下降的高度小于某个定义的值,则停止下降;
算法:

特点:
(1)初始点不同,获得的最小值也不同,因此梯度下降求得的只是局部最小值;
(2)越接近最小值时,下降速度越慢;
问题:如果初始值就在local minimum的位置,则会如何变化?
答:因为已经在local minimum位置,所以derivative 肯定是0,因此不会变化;
如果取到一个正确的值,则cost function应该越来越小;
问题:怎么取值?
答:随时观察值,如果cost function变小了,则ok,反之,则再取一个更小的值;
下图就详细的说明了梯度下降的过程:

从上面的图可以看出:初始点不同,获得的最小值也不同,因此梯度下降求得的只是局部最小值;
注意:下降的步伐大小非常重要,因为如果太小,则找到函数最小值的速度就很慢,如果太大,则可能会出现overshoot the minimum的现象;
下图就是overshoot minimum现象:

如果Learning rate取值后发现J function 增长了,则需要减小Learning rate的值;
Integrating with Gradient Descent & Linear Regression
梯度下降能够求出一个函数的最小值;
线性回归需要求出,使得cost function的最小;
因此我们能够对cost function运用梯度下降,即将梯度下降和线性回归进行整合,如下图所示:

梯度下降是通过不停的迭代,而我们比较关注迭代的次数,因为这关系到梯度下降的执行速度,为了减少迭代次数,因此引入了Feature Scaling;
Feature Scaling
此种方法应用于梯度下降,为了加快梯度下降的执行速度;
思想:将各个feature的值标准化,使得取值范围大致都在-1<=x<=1之间;
常用的方法是Mean Normalization,即
或者:
[X-mean(X)]/std(X);
举个实际的例子,
有两个Feature:
(1)size,取值范围0~2000;
(2)#bedroom,取值范围0~5;
则通过feature scaling后,
练习题
我们想要通过期中开始成绩预测期末考试成绩,我们希望得到的方程为:
给定以下训练集:
midterm exam (midterm exam)2 final exam
89 7921 96
72 5184 74
94 8836 87
69 4761 78
我们想对(midterm exam)^2进行feature scaling,则经过feature scaling后的值为多少?
max = 8836,min=4761,mean=6675.5,则x=(4761-6675.5)/(8836-4761) = -0.47;
多变量线性回归
前面我们只介绍了单变量的线性回归,即只有一个输入变量,现实世界不可能这么简单,因此此处我们要介绍多变量的线性回归;
举个例子:
房价其实由很多因素决定,比如size、number of bedrooms、number of floors、age of home等,这里我们假设房价由4个因素决定,如下图所示:

我们前面定义过单变量线性回归的模型:

这里我们可以定义出多变量线性回归的模型:

Cost function如下:

如果我们要用梯度下降解决多变量的线性回归,则我们还是可以用传统的梯度下降算法进行计算:

总练习题:
1.我们想要根据一个学生第一年的成绩预测第二年的成绩,x为第一年得到A的数量,y为第二年得到A的数量,给定以下数据集:
x y
3 4
2 1
4 3
0 1
(1)训练集的个数是多少? 4个;
(2)J(0,1)的结果是多少?
J(0,1) = 1/(2*4)*[(3-4)^2+(2-1)^2+(4-3)^2+(0-1)^2] = 1/8*(1+1+1+1) = 1/2 = 0.5;
我们也可以通过vectorization的方法快速算出J(0,1):
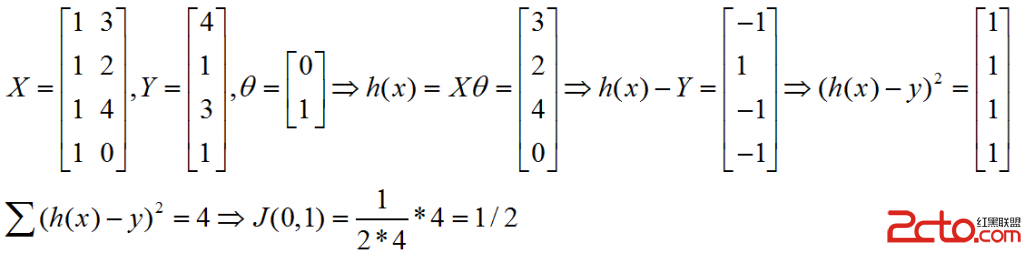
补充:综合编程 , 其他综合 ,