HDU1556 color the ball][树状数组]解题报告
时间复杂度为什么是log(n)?
首先树状数组的思想本身就是一个树,所以在操作的时间复杂度上面和树相似
还可以通过计算来论证:
假设现在的节点是n,那么到达父节点的方法就是:
n=n+n&-n (不知道为什么这样写的,自行百度)
实际上就是把n的二进制最左边的1向左移动了一位,比如2-10,4-100
到达子节点的方法就是:
n=n-n&-n
这个实际上就是每次把最左边的1变成0,比如7-111,6-110,4-100
那么这样二进制的位移运算的时间复杂度是log(n),所以树状数组查询和统计的时间复杂度也为log(n)
解题思路
这道题可以用很多方法来做,线段树是最容易想到的,但是代码实现上很复杂
其实这道题可以把每次染色的点抽象为每次涂改的区间,然后对要查询的点所在区间的更新次数进行求和
这样就可以在时间上,大大缩短,查询和统计的时间复杂度都为log(n)
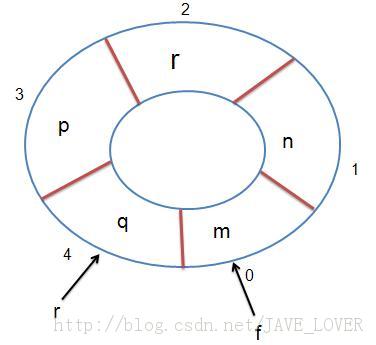
树状数组中的每个节点都代表了一段线段区间,每次更新的时候,根据树状数组的特性可以把b以前包含的所有区间都找出来,然后把b以前的区间全部加一次染色次数。然后,再把a以前的区间全部减一次染色次数,这样就修改了树状数组中的[a,b]的区间染色次数,查询每一个点总的染色次数的时候,就可以直接向上统计每个父节点的值,就是包含这个点的所有区间被染色次数,这就是树状数组中向下查询,向上统计的典型应用
Ps:根据个人理解层次的不同,这道题也可以向上查询,向下统计,还可以向下查询,向下统计,不过我写的这种是最容易理解的
代码实现如下:
用cin,cout进行读写操作的话,会超时,所以我还是用的scanf(),printf()
[cpp]
#include <stdio.h>
#include <string.h>
const int MAXN=110000;
int n,c[MAXN];
int lowbit(int x)
//计算2^k
{
x=x&-x;
return x;
}
void update(int num,int val)
//向下查询,num是要更新的子节点,val是要修改的值
{
while(num>0)
{
c[num]+=val;
num-=lowbit(num);
}
}
int getSum(int num)
//向上统计每个区间被染色的次数
{
int sum=0;
while(num<=n)
{
sum+=c[num];
num+=lowbit(num);
}
return sum;
}
int main()
{
int a,b;
while(scanf("%d",&n),n)
{
memset(c,0,sizeof(c));
for(int i=0;i<n;i++)
{
scanf("%d%d",&a,&b);
//将b以下区间+1
update(b,1);
//将a以下区间-1
update(a-1,-1);
}
for(int j=1;j<n;j++)
{
printf("%d ",getSum(j));
}
printf("%d\n",getSum(n));
}
return 0;
}
#include <stdio.h>
#include <string.h>
const int MAXN=110000;
int n,c[MAXN];
int lowbit(int x)
//计算2^k
{
x=x&-x;
return x;
}
void update(int num,int val)
//向下查询,num是要更新的子节点,val是要修改的值
{
while(num>0)
{
c[num]+=val;
num-=lowbit(num);
}
}
int getSum(int num)
//向上统计每个区间被染色的次数
{
int sum=0;
while(num<=n)
{
sum+=c[num];
num+=lowbit(num);
}
return sum;
}
int main()
{
int a,b;
while(scanf("%d",&n),n)
{
memset(c,0,sizeof(c));
for(int i=0;i<n;i++)
{
scanf("%d%d",&a,&b);
//将b以下区间+1
update(b,1);
//将a以下区间-1
update(a-1,-1);
}
for(int j=1;j<n;j++)
{
printf("%d ",getSum(j));
}
printf("%d\n",getSum(n));
}
return 0;
}
补充:软件开发 , C++ ,