超高速计算n以内素数个数(百亿内3毫秒解决)
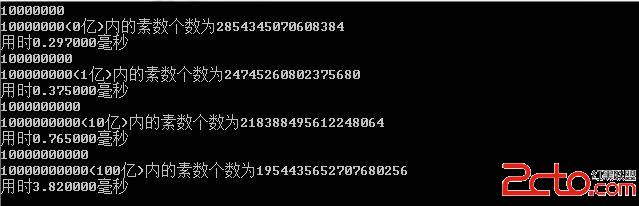
判断n以内素数个数有很多算法,最简单的是循环直接判断,这个效率不用说,n稍大就不行了。最流行的是筛选法,原理就是定义一个素数标志位表,初始为1,遇到一个数如果对应标志位为1判断这个数是不是素数,是将该为置1,不是放0,然后将他的倍数位置全部置0,然后继续。。这个效率还是比较快的,但是计算到10^8时候需要3s左右了,对于一般要求基本够了,但是对于ACM里面对时间要求很严还是不够。可以对帅选法进行优化,不如偶数直接跳过,以后直接加偶数倍,甚至加入移位运算判断是不是3的倍数,5的倍数等等,最后基本勉强在ACM要求的时间之内。下来介绍一种逆天的算法:MEISSEL-LEHMER,布吉岛的可以百度下。不容易看懂。。。。。。先看下效果绝对碉堡!!!!
代码如下:
[cpp]
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>
__int64 *primarr, *v;
__int64 q = 1, p = 1;
//π(n)
__int64 pi(__int64 n, __int64 primarr[], __int64 len)
{
__int64 i = 0, mark = 0;
for (i = len - 1; i > 0; i--) {
if (primarr[i] < n) {
mark = 1;
break;
}
}
if (mark)
return i + 1;
return 0;
}
//Φ(x,a)
__int64 phi(__int64 x, __int64 a, __int64 m)
{
if (a == m)
return (x / q) * p + v[x % q];
if (x < primarr[a - 1])
return 1;
return phi(x, a - 1, m) - phi(x / primarr[a - 1], a - 1, m);
}
__int64 prime(__int64 n)
{
char *mark;
__int64 mark_len;
__int64 count = 0;
__int64 i, j, m = 7;
__int64 sum = 0, s = 0;
__int64 len, len2, len3;
mark_len = (n < 10000) ? 10002 : ((__int64)exp(2.0 / 3 * log(n)) + 1);
//筛选n^(2/3)或n内的素数
mark = (char *)malloc(sizeof(char) * mark_len);
memset(mark, 0, sizeof(char) * mark_len);
for (i = 2; i < (__int64)sqrt(mark_len); i++) {
if (mark[i])
continue;
for (j = i + i; j < mark_len; j += i)
mark[j] = 1;
}
mark[0] = mark[1] = 1;
//统计素数数目
for (i = 0; i < mark_len; i++)
if (!mark[i])
count++;
//保存素数
primarr = (__int64 *)malloc(sizeof(__int64) * count);
j = 0;
for (i = 0; i < mark_len; i++)
if (!mark[i])
primarr[j++] = i;
if (n < 10000)
return pi(n, primarr, count);
//n^(1/3)内的素数数目
len = pi((__int64)exp(1.0 / 3 * log(n)), primarr, count);
//n^(1/2)内的素数数目
len2 = pi((__int64)sqrt(n), primarr, count);
//n^(2/3)内的素数数目
len3 = pi(mark_len - 1, primarr, count);
//乘积个数
j = mark_len - 2;
for (i = (__int64)exp(1.0 / 3 * log(n)); i <= (__int64)sqrt(n); i++) {
if (!mark[i]) {
while (i * j > n) {
if (!mark[j])
s++;
j--;
}
sum += s;
}
}
free(mark);
sum = (len2 - len) * len3 - sum;
sum += (len * (len - 1) - len2 * (len2 - 1)) / 2;
//欧拉函数
if (m > len)
m = len;
for (i = 0; i < m; i++) {
q *= primarr[i];
p *= primarr[i] - 1;
}
v = (__int64 *)malloc(sizeof(__int64) * q);
for (i = 0; i < q; i++)
v[i] = i;
for (i = 0; i < m; i++)
for (j = q - 1; j >= 0; j--)
v[j] -= v[j / primarr[i]];
sum = phi(n, len, m) - sum + len - 1;
free(primarr);
free(v);
return sum;
}
int main()
{
__int64 n;
__int64 count;
int h;
clock_t start, end;
while(scanf("%I64d", &n)!=EOF)
{
p=1;
q=1;
start = clock();
count = prime(n);
end = clock() - start;
printf("%I64d(%d亿)内的素数个数为%I64d\n",n,n/100000000,count);
printf("用时%lf毫秒\n",(double)end/1000);
}
return 0;
}
补充:软件开发 , C++ ,