poj_2255_Tree Recovery_解题报告
题意:输入两组数据,分别是前序遍历序列和中序遍历序列,你需要编写程序通过这两组数据求出该树的后序遍历序列(前序序列 + 中序序列 = 后序序列)解法:递归
题目分析:
可以先按照用笔和纸的形式去推导出后序序列。推导过程省略,在推导过程中我们会发现规律:
假设 前序序列是 A B E H F C G I
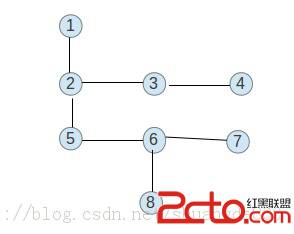
中序序列是 H E B F A C I G (图如下)

每一次从前序序列里,按顺序抽取出字母就能将中序序列分割,并根据中序遍历的特性。分割后的两部分分别是 左子树 和 右子树(注意,他们也是二叉树!)
就像这样:取A, 中序序列被分割为 左子树:H E B F 右子树 C I G
继续取B,但是这次是对左子树:H E B F 进行分割。 分割结果是: 左子树:H E 右子树 B F
直到不能再分割,递归会返回去到第一次使用 A 分割出来的 右子树 里继续分割
上述整个过程都是递归,所以结合代码和用纸笔画一次会更好理解
代码:
[cpp]
#include <stdio.h>
#include <stdlib.h>
typedef struct TreeNode
{
char data;
struct TreeNode *lchild;
struct TreeNode *rchild;
} Node, *PNode;
char preorder[28]; //存放前序序列
char infix[28]; //存放中序序列
char *Pr;
void build(char *in, char *pr, PNode *tr);
void postordertraversal(PNode T);
int main()
{
//先建树、再后序遍历输出
PNode T;
while(scanf("%s %s", &preorder[1], &infix[1]) == 2)
{
build(&infix[1], &preorder[1], &T);
postordertraversal(T);
printf("\n");
}
return 0;
}
void build(char *in, char *pr, PNode *tr)
{
char *p = in;
Pr = pr;
if (*in == 0)
{
*tr = NULL;
return;
}
while (1)
{
if (*in == *Pr)
{
(*tr) = (PNode)malloc(sizeof(Node));
(*tr)->data = *Pr;
*in = 0;
break;
}
in++;
}
Pr = Pr + 1;
build(p, Pr, &(*tr)->lchild);
build(in+1, Pr, &(*tr)->rchild);
}
void postordertraversal(PNode T)
{
if (T == NULL)
return;
postordertraversal(T->lchild);
postordertraversal(T->rchild);
printf("%c", T->data);
}
这份代码有些东西需要注意:
这里使用到指针,其实可以不使用指针的,下面介绍的更精巧的解法就是用下标的。能尽量不用指针就尽量不用
注意指向指针的指针在这里的作用,这里有讲解
上面的解法是比较直接容易想到的,所以代码没有很精巧。而这里有份更好的解法!
补充:软件开发 , C++ ,