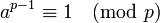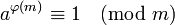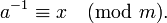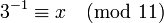RSA算法从数学基础到实例全面解析

1、同余（合同式）

两个整数a，b，若它们除以正整数m所得的余数相等，则称a，b对于模m同余

记作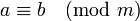 $a \equiv b \pmod{m}$

例如1≡13 (mod 12),可以理解为时钟上1点和13点的指针位置相同

重要性质

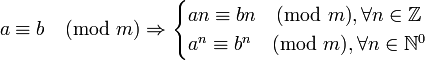
$a \equiv b \pmod{m} \Rightarrow \begin{cases} an \equiv bn \pmod{m}, \forall n \in \mathbb{Z} \\ a^n \equiv b^n \pmod{m}, \forall n \in \mathbb{N}^0\end{cases}$

例如1^5=1，13 ^5=371293=30941*12+1

即1^5≡1≡13 ^5(mod 12)

2、欧拉函数（Euler's totient function）

欧拉函数 φ(n)是少于或等于n的数中与n互质的数的数目，例如φ(9) = 6，因为比9小的数中与9互质的有1, 2, 4, 5, 7,8六个数，所以9的欧拉函数为6。

计算方法：

将n分解为质数相乘的形式

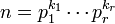$n = p_1^{k_1} \cdots p_r^{k_r}$ ，每个p_i都是质数

则欧拉函数

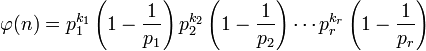
$\varphi(n) = p_1^{k_1} \left(1- \frac{1}{p_1} \right) p_2^{k_2} \left(1- \frac{1}{p_2} \right) \cdots p_r^{k_r} \left(1- \frac{1}{p_r} \right)$

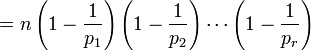
$=n \left(1- \frac{1}{p_1} \right)\left(1- \frac{1}{p_2} \right) \cdots\left(1- \frac{1}{p_r} \right)$

例如

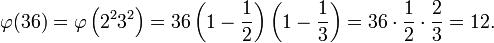
$\varphi(36)=\varphi\left(2^2 3^2\right)=36\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)=36\cdot\frac{1}{2}\cdot\frac{2}{3}=12.$

两条结论

若n为质数，则φ(n)=n-1

若m与n互质，则 φ(mn) = φ(m)φ(n)

3、费马小定理与欧拉定理

费马小定理

若a为整数，p为质数则

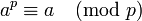
$a^p \equiv a \pmod{p}$

如果a不是p的倍数,可写为

$a^{p-1} \equiv 1 \pmod{p}$

推广：欧拉定理

对任何两互质正整数a, m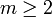， $m\ge2$ ，有

4、模反

$a^{\varphi(m)} \equiv 1 \pmod m$

$a^{-1} \equiv x \pmod{m}.$

或写成

$ax \equiv aa^{-1} \equiv 1 \pmod{m}.$

例如

$3^{-1} \equiv x \pmod{11}$

$3x \equiv 1 \pmod{11}$

当x=4时上式成立，所以4是3的模反，

注意：4并不是唯一的解，在4的基础上加上模（11）的倍数依然满足上式，例如15,26,37,48等

但是寻找这样的x并不是一目了然，可以用下面的扩展欧几里得算法。

5、扩展欧几里得算法
作为欧几里得算法的扩展，寻找的是满足ax + by = 易做图(a,b)的x和y。

当a,b互质时，可以看出x是a在b模下的反(ax=1(mod y)) ;可以看出y是b在a模下的反(by=1(mod x))

我用python写了一个递归实现

def extended_易做图(a, b):
    if (b == 0):
        return (1, 0)
    else:
        q, r = a/b,a%b
        s, t = extended_易做图(b, r)
        return (t, s - q * t)

运行实例，还是拿上面的例子，求3在模11下的反

print extended_易做图(3,11)

得到结果：

(4, -1)

意即4*3+(-1)*11=1

因此可得的解为4

6、密钥生成
选取两个素数p和q

计算n=pq

计算φ(n) = (p – 1)(q – 1) （可由2中的两个结论推出）

选取e使得 1 < e < φ(n)且e与φ(n)互质，e和n作为公钥

计算 d = e–1 mod φ(n); d和n作为密钥

7、加密
将公钥(n,e)传送给对方，自己保留密钥。对方对明文进行加密。

明文m，密文c，由密钥(n,e)可得

c = me (mod n).

8、解密
收到对方传过来的密文c后可以用密钥(d,n)进行解密，得到明文m

m = cd (mod n).

9、实现
用python把流程走一遍

>>> from Euclid_Ex import extended_易做图
#导入上面定义的扩展欧几里得算法
>>> p,q=61,53
#定义p,q,并求得n和phi
>>> n=p*q
>>> n
3233
>>> phi=(p-1)*(q-1)
>>> phi
3120
#选择17作为公钥
>>> e=17
#计算密钥
>>> extended_易做图(e,phi)
(-367, 2)
#计算得到的是负数，不是我们所想要的，按照之前提过的，只要加上模就可以了
>>> -367+phi
2753
#得到了密钥为2753
>>> d=2753
#在此已经得到了加密和解密所需要

补充：软件开发 , 其他 ,