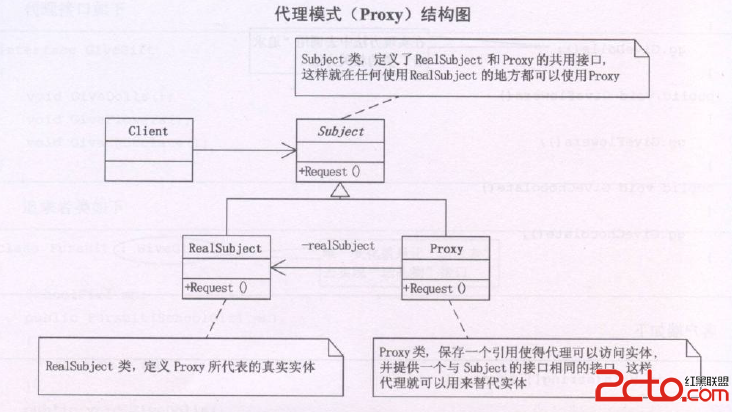
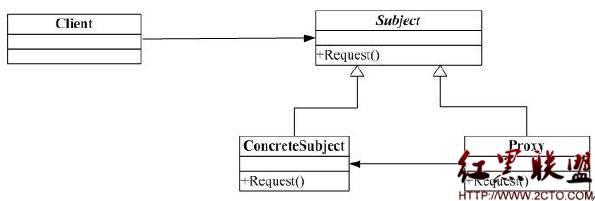
(大素数2.1.2.1)UVA 10871 Primed Subsequence(欧拉筛法)

 
 * UVA_10871.cpp 
 * 
 *  Created on: 2013年10月7日 
 *      Author: Administrator 
 */  
  
#include <iostream>  
#include <cstdio>  
#include <cstring>  
  
using namespace std;  
  
const int maxn = 10011;  
bool u[maxn];  
int su[maxn];  
int num = 0;  
  
void prepare() {  
    int i, j;  
    memset(u, true, sizeof(u));  
  
    for (i = 2; i < maxn; ++i) {  
        if (u[i]) {  
            su[++num] = i;  
        }  
  
        for (j = 1; j <= num; ++j) {  
            if (i * su[j] > maxn) {  
                break;  
            }  
  
            u[i * su[j]] = false;  
  
            if (i % su[j] == 0) {  
                break;  
            }  
        }  
    }  
}  
  
bool pri(int x) {  
    if (x <= 10010) {  
        return u[x];  
    }  
  
    int i;  
    for (i = 1; i <= num; ++i) {  
        if (x % su[i] == 0) {  
            return false;  
            break;  
        }  
    }  
  
    return true;  
}  
  
int main() {  
    prepare();  
  
    int t;  
    scanf("%d", &t);  
    while (t--) {  
        int n;  
        scanf("%d", &n);  
  
        int i, j;  
        int s[n + 1];  
        s[0] = 0;  
        for (i = 1; i <= n; ++i) {  
            scanf("%d", &s[i]);  
            s[i] += s[i - 1];  
        }  
  
        bool ok = false;  
        for (i = 2; i <= n; ++i) {  
            for (j = 1; j + i - 1 <= n; ++j) {  
                int k = s[i + j - 1] - s[j - 1];  
                if (pri(k)) {  
                    ok = true;  
                    printf("Shortest primed subsequence is length %d:", i);  
  
                    for (k = 1; k <= i; ++k) {  
                        printf(" %d", s[j + k - 1] - s[j + k - 2]);  
                    }  
                    printf("\n");  
  
                    break;  
  
                }  
            }  
  
            if (ok) {  
                break;  
            }  
  
        }  
  
        if (!ok) {  
            printf("This sequence is anti-primed.\n");  
        }  
    }  
  
    return 0;  
}  

补充：软件开发 , C++ ,

上一个：C++小知识之Map用法
下一个：hdu4576Robot