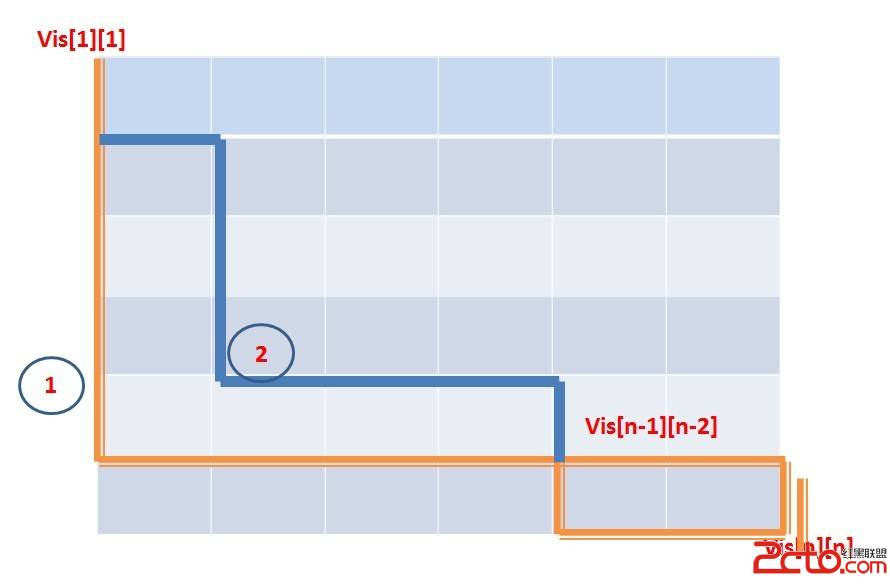
HDU 4160 最小路径覆盖 = 顶点数 - 最大匹配数 二分匹配

#include<stdio.h>  
#include<string.h>  
  
#define N 600  
  
struct Edge{  
    int to, nex;  
}edge[N*N];  
int head[N*2], edgenum;  
void addedge(int u, int v){  
    Edge E = { v, head[u] };  
    edge[ edgenum ] = E;  
    head[u] = edgenum ++;  
}  
  
struct node{  
    int a,b,c;  
}p[N];  
  
int n;  
  
int lef[N*2];  
bool T[N*2];  
  
int match(int x){  
    for(int i = head[x]; i != -1; i = edge[i].nex){  
        int v = edge[i].to;  
        if(T[v])continue;  
        T[v] = true;  
        if(lef[v] == -1 || match( lef[v] ) )  
        {  
            lef[v] = x;  
            return true;  
        }  
    }  
    return false;  
}  
  
  
int solve(){  
    int ans = 0;  
    memset(lef, -1, sizeof(lef));  
    for(int i = 1; i <= n; i++)  
    {  
        memset(T, 0, sizeof(T));  
        ans += match( i );  
    }  
    return ans;  
}  
  
void init(){  
    memset(head, -1, sizeof(head)),     edgenum = 0;  
  
    for(int i = 1; i <= n; i++)  
        scanf("%d %d %d", &p[i].a, &p[i].b, &p[i].c);  
  
    for(int i = 1; i <= n; i++)  
        for(int j = 1; j <= n; j++)  
        {  
            if(p[i].a < p[j].a && p[i].b < p[j].b && p[i].c < p[j].c)  
                addedge(i, j + N);  
        }  
}  
  
int main(){  
    int  m, u, v;  
    while(~scanf("%d",&n), n){  
        init();  
        printf("%d\n", n - solve());  
    }  
    return 0;  
}  
/* 
3 
5 4 8 
27 10 10 
100 32 523 
3 
1 2 1 
2 1 1 
1 1 2 
4 
1 1 1 
2 3 2 
3 2 2 
4 4 4 

0 

*/