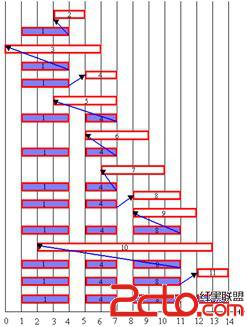
sgu 176. Flow construction

题目大意：网中有些边必须满流，求最小可行流

题目思路：有上下界最小流，见周源《一种简易的方法求解流量有上下界的网络中网络流问题》，还有一种非二分的方法，但没有严格证明，所以我还是用的二分。

[cpp]
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<string>
#include<queue>
#include<algorithm>
#include<vector>
#include<stack>
#include<list>
#include<iostream>
#include<map>
using namespace std;
#define inf 0x3f3f3f3f
#define Max 110
int max(int a,int b)
{
    return a>b?a:b;
}
int min(int a,int b)
{
    return a<b?a:b;
}
int dis[Max],gap[Max],pre[Max],cur[Max],p[Max];
//int d[4][2]={0,1,1,0,0,-1,-1,0};
int in[Max],out[Max],id[Max*Max];
int n,m,s,t,eid;
int c[Max*Max];
struct node
{
     int to,next,c;
}e[2*Max*Max],ee[2*Max*Max];
void addedge(int u,int v,int c)
{
    ee[eid].to=v;
    ee[eid].c=c;
    ee[eid].next=p[u];
    p[u]=eid++;
}
int ISAP(int st,int ed,int n,int count)   ///起点，终点，顶点数
{
    memset(dis, 0, sizeof(dis));
    memset(gap, 0, sizeof(gap)); gap[0]=n;
    memcpy(cur, p, sizeof(p));      ///memcpy!
    int i,flag,v,u=pre[st]=st,maxflow=0,aug=inf; //puts("akk");
    while(dis[st] < n)
    {
        for(flag=0,i=cur[u];i!=-1; i=e[i].next) /// cur[u]
            if(e[i].c&& dis[u] == dis[e[i].to]+1)
            {
                flag = 1;

                break;
            }
        if(flag)
        {
            if(aug > e[i].c)
                aug = e[i].c;
            v = e[i].to;
            pre[v] = u;
            cur[u] = i;
            u = v;
            if(u == ed)
            {
                for(u=pre[u]; 1;u=pre[u])    ///notice!
                {
                    e[cur[u]].c -= aug;
                    e[cur[u]^1].c += aug;
                    if(u==st) break;
                   // puts("akkk");
                }
                maxflow += aug;
                aug = inf;
            }
        }
        else
        {
            int minx = n;
            for(i=p[u]; i!=-1; i=e[i].next)
                if(e[i].c&& dis[e[i].to]<minx)
                {
                    minx = dis[e[i].to];
                    cur[u] = i;
                }
            if(--gap[dis[u]] == 0)
                break;
            dis[u] = minx+1;
            gap[dis[u]]++;
            u = pre[u];
        }
    }
// printf("Case %d:\n%d\n",count,maxflow);
   // printf("%d\n",maxflow);
    return maxflow;
}
int main()
{
    int m,n,t,count=1,sum;
    int u,v,i,j,k,x,y,tp;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        memset(p,-1,sizeof(p));
        eid=0;
        sum=0;
        memset(in,0,sizeof(in));
        memset(out,0,sizeof(out));
        memset(id,-1,sizeof(id));
        for(i=0;i<m;i++)
        {
            scanf("%d%d%d%d",&u,&v,&c[i],&tp);
            if(tp==1)
            {
                in[v]+=c[i];
                su

补充：软件开发 , C++ ,