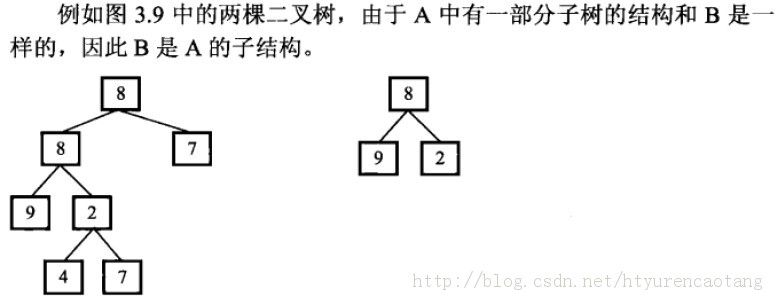
hdu 3030 Increasing Speed Limits（树状数组求最长上升子序列）

在前边关于DP总结的文章中说了通过普通的DP法个二分查找法求最长上升子问题，最近在学习BIT，然后突然发现原来通过BIT也可以求最长上
 
升子序列问题。本来想着可以通过类似的方法在O(nlogn)时间内求出，然而题目的意思是求出总和，这样的话二分法就不好使了，一开始也没
 
有理解，不过通过单纯的求最长上升子序列，终于搞明白了。
 
先来看看求解普通的最长上升子序列问题：
 
题目中首先将重复的元素去掉，以为我们求的是严格意义上的上升序列，因此，相同的元素是没有任何意义的，所以先对所有元素排序，然后
 
去除掉重复元素。
 
[cpp]  
#include<iostream>  
#include<cstdio>  
#include<cstring>  
#include<algorithm>  
  
using namespace std;  
  
const int N=110000;  
  
int n,val[N],a[N];  
int len,arr[N];  
  
int lowbit(int x){  
    return x&(-x);  
}  
//原始的update  
void update(int i,int x){  
    while(x<=len){  
        if(i>arr[x])  
            arr[x]=i;  
        x+=lowbit(x);  
    }  
}  
  
int query(int x){  
    int ans=0;  
    while(x){  
        if(arr[x]>ans)  
            ans=arr[x];  
        x-=lowbit(x);  
    }  
    return ans;  
}  
  
int main(){  
    while(~scanf("%d",&n)){  
        for(int i=0;i<n;i++){  
            scanf("%d",&val[i]);  
            a[i]=val[i];  
        }//排序去冲  
        sort(a,a+n);  
        len=unique(a,a+n)-a;  
        memset(arr,0,sizeof(arr));  
        int ans=1,tmp;  
        for(int i=0;i<n;i++){//这里val中保存的是可以插入元素的位置  
            val[i]=lower_bound(a,a+len,val[i])-a;  
            tmp=query(val[i])+1;//tmp保存的是当前位置左边比它小的数的个数，注意这里要加1，因为第i结束时需要给序列加1  
            if(tmp>ans)//取最大值，我们求得是最长上升的序列  
                ans=tmp;  
            update(tmp,val[i]+1);更新val[i]+1位置，注意tree中保存的是左边小的值，所以在真正求值时需要+1  
        }  
        printf("%d\n",ans);  
    }  
    return 0;  
}  
 
好了，搞明白了找个基本问题，杭电的这道题也就可以理解了：
 
[cpp]  
#include <cstdlib>  
#include <cstring>  
#include <cstdio>  
#include <map>  
#include <algorithm>  
#define MOD 1000000007  
#define MAXN 500005  
using namespace std;   
  
int num[MAXN], A[MAXN], c[MAXN], seq[MAXN], cnt;  
  
inline int lowbit(int x)  
{  
    return x & -x;  
}  
  
//这里的update是正常的  
inline void update(int pos, int val)  
{  
    for (int i = pos; i <= cnt; i += lowbit(i))  
    {   
        c[i] += val;  
        if (c[i] >= MOD)  
            c[i] %= MOD;  
    }  
}  
  
inline int getsum(int pos)  
{  
    int s = 0;  
    for (int i = pos; i > 0; i -= lowbit(i))  
    {  
        s += c[i];  
        if (s >= MOD)  
            s %= MOD;  
    }  
    return s;  
}  
  
int main()  
{  
    int T, n, m;  
    long long X, Y, Z, res;   
    scanf("%d", &T);  
    for (int ca = 1; ca <= T; ++ca)  
    {  
        res = 0;  
        map<int,int>mp;  
        scanf("%d %d %I64d %I64d %I64d", &n, &m, &X, &Y, &Z);  
        memset(c, 0, sizeof (c));  
        for (int i = 0; i < m; ++i)  
        {  
            scanf("%d", &A[i]);  
        }  
        for (int i = 0; i < n; ++i)  
        {  
            num[i+1] = A[i%m];  
            seq[i] = num[i+1];  
            A[i%m] = (X*A[i%m]+Y*(i+1))%Z;  
        }  
        //其中num和seq保存的值是一模一样的  
        sort(num+1, num+1+n);  
        //去除临近元素，cnt表示的是一共有多少个不同的元素  
        //这里进行的是离散化的操作，对于最长上升子序列来说，相同元素是毫无意义的  
        cnt = unique(num+1, num+1+n) - (num+1);  
        for (int i = 1; i <= cnt; ++i)  
        {//上边是通过二分找位置，这里使用的map来记录位置   
            mp[num[i]] = i;  
        }  
        update(1, 1);  
        for (int i = 0; i < n; ++i)  
        { //注意这里是累加，而上边的代码中是取最大值  
            long long x = getsum(mp[seq[i]]);   
            res += x;  
            if (res > MOD)

补充：软件开发 , C++ ,