活动选择问题的实现(动态规划 和 贪心)
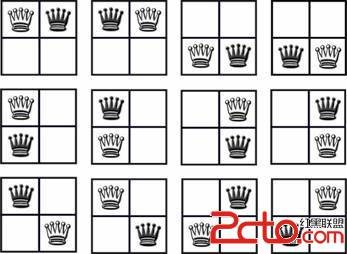
问题叙述:如下图表示活动的开始和结束时间,s[i],开始时间;f[j]结束时间。现在要进行一些列如下活动,注意每个时间段只能进行一场活动,也就是活动不能同时进行,要求举行的活动次数最多。求调度方法。
老规矩,动态规划,要找出两个问题:
1,子问题的最优解;
2,子问题是什么。
abviously,本问题的最优解为:活动数的次数最多,子问题是:看递推公式
设c[i]为第i个 位置处的活动次数.......做不出来了,以后补充。
本想用动态规划试试做做,操蛋的做不出来,算了还是贪心吧,毕竟贪心最简单对于活动调度,不过有个证明过程。先上代码吧。
[cpp]
#include<iostream>
using namespace std;
//s 活动开始时间的数组,f活动结束时间的数组,n 数组的大小;
const int N=11;
void GreedySelector(int* s,int* f,int n )
{
bool A[N];
A[0]=true;
int j=0;
for(int i=1;i<N;++i)
{
if(s[i]>f[j])
{
A[i]=true;
j=i;
}
else
{
A[i]=false;
}
}
for(int k=0;k<N;++k)
{
if(A[k]==true)
cout<<k<<" ";
}
}
int main()
{
int s[N]={1,3,0,5,3,5,6,8,8,2,12};//活动的开始时间
int f[N]={4,5,6,7,8,9,10,11,12,13,14};//活动的结束时间
GreedySelector( s, f, N );
return 0;
}
#include<iostream>
using namespace std;
//s 活动开始时间的数组,f活动结束时间的数组,n 数组的大小;
const int N=11;
void GreedySelector(int* s,int* f,int n )
{
bool A[N];
A[0]=true;
int j=0;
for(int i=1;i<N;++i)
{
if(s[i]>f[j])
{
A[i]=true;
j=i;
}
else
{
A[i]=false;
}
}
for(int k=0;k<N;++k)
{
if(A[k]==true)
cout<<k<<" ";
}
}
int main()
{
int s[N]={1,3,0,5,3,5,6,8,8,2,12};//活动的开始时间
int f[N]={4,5,6,7,8,9,10,11,12,13,14};//活动的结束时间
GreedySelector( s, f, N );
return 0;
}
测试结果:
证明略,没怎么明白,智商啊,亵渎了 我的大脑袋。
把算法导论的证明贴出来吧:
再来做个例子吧:
背包问题:
0-1背包问题:有一个窃贼在一家商店时发现有n件物品,第i件物品值vi元,重wi磅。此处,vi,wi都是整数,。他希望带走的东西越值钱越好,但他的背包中至多只能装下W磅。
,W为一整数。应该带走那几样东西呢?(0-1的意思是:物品或被带走,或被留下,不能带走一部分,留下一部分)
部分背包问题:场景与上面类似,但是窃贼可以带走物品的一部分,而不必做出0-1的二分选择。
下面一个个来解决吧。
0-1:
我自己参照写的代码:
[cpp]
#include<iostream>
using namespace std;
//w 物品的重量,v物品的价值,count物品的数量,m是背包最大的容量
void processing(int* w,int* v,int count,int m,int(* c)[11])
{
for(int i=1;i<=count;++i)
for(int j=1;j<=m;++j)
{
if(w[i]<=j)//可以放对应的背包了
{
if(c[i-1][j]>c[i-1][j-w[i]]+v[i])
c[i][j]=c[i-1][j];
else
c[i][j]=c[i-1][j-w[i]]+v[i];
}
else
{
c[i][j]=c[i-1][j];
}
}
}
void Printf(int count,int m,int (*c)[11],int* log,int *w)
{
int j=m;
for(int i=count;i>=1;--i)
if(c[i][j]==c[i-1][j])
log[i]=0;
else
{
log[i]=1;
j=j-w[i];
}
}
int main()
{
int w[4]={0,3,4,5};
int v[4]={0,4,5,6};
int c[4][11];
int log[4];
int count=3;
int m=10;
for(int i=0;i<=3;++i)
for(int j=0;j<=10;++j)
c[i][j]=0;
processing(w, v,3,10,c);
Printf(3,10,c,log,w);
cout<<"装入的物品为:";
for(int i=1;i<=count;++i)
if(log[i]==1)cout<<i<<" ";
cout<<"总价值为:"<<c[count][m];
}
#include<iostream>
using namespace std;
//w 物品的重量,v物品的价值,count物品的数量,m是背包最大的容量
void processing(int* w,int* v,int count,int m,int(* c)[11])
{
for(int i=1;i<=count;++i)
for(int j=1;j<=m;++j)
{
if(w[i]<=j)//可以放对应的背包了
{
if(c[i-1][j]>c[i-1][j-w[i]]+v[i])
c[i][j]=c[i-1][j];
else
c[i][j]=c[i-1][j-w[i]]+v[i];
&nb
补充:软件开发 , C++ ,