UVA 11538 - Chess Queen

Problem A

Chess Queen

Input: Standard Input

Output: Standard Output

You probably know how the game of chess is played and how chess queen operates. Two chess queens are in attacking position when they are on same row, column or diagonal of a chess board. Suppose two such chess queens (one black and the other white) are placed on (2x2) chess board. They can be in attacking positions in 12 ways, these are shown in the picture below:

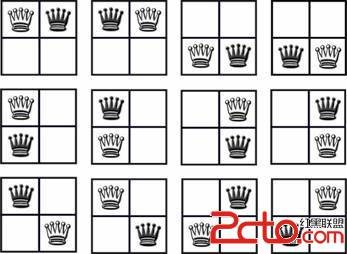
Figure: in a (2x2) chessboard 2 queens can be in attacking position in 12 ways

Given an (NxM) board you will have to decide in how many ways 2 queens can be in attacking position in that.

Input

Input file can contain up to 5000 lines of inputs. Each line contains two non-negative integers which denote the value of M and N (0< M, N£106) respectively.

Input is terminated by a line containing two zeroes. These two zeroes need not be processed.

Output

For each line of input produce one line of output. This line contains an integer which denotes in how many ways two queens can be in attacking position in an (MxN) board, where the values of M and N came from the input. All output values will fit in 64-bit signed integer.

Sample Input Output for Sample Input

2 2

100 223

2300 1000

0 0

10907100

11514134000

Problemsetter: Shahriar Manzoor

Special Thanks to: Mohammad Mahmudur Rahman

m行n列的表格

1、在同一行互相攻击的方案：n*m*(n-1)

2、在同一列互相攻击的方案：n*m*(m-1)

3、在同一斜线互相攻击的方案：以 m<n 为例 { sum{ for( i=1;i<=n-1;i++) i*(i-1) } *2 + [n-(m-1)]*m*(m-2) } *2 , 大于则交换 m,n

#include <iostream>  
#include <cstdio>  
#include <algorithm>  
using namespace std;  
  
unsigned long long n,m,sum;  
  
int main(){  
    while(cin>>m>>n && (m||n)){  
        sum=m*n*(n-1) + m*n*(m-1);  
        if(n<m) swap(n,m);  
        sum+=m*(m-1)*(m-2)/3*4;  
        sum+=(n+1-m)*m*(m-1)*2;  
        cout<<sum<<endl;  
    }  
    return 0;  
}

补充：软件开发 , C++ ,