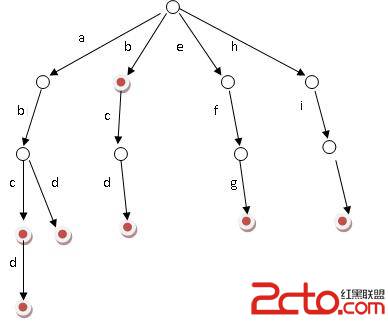
二叉树的各种操作复习

[cpp]
/*二叉树的各种操作复习*/
#include <stdio.h>

#define BACK_ODER   -1
#define IN_ODER     0
#define PRE_ODER    1
#define LEVEL_ODER 2//层次化遍历
typedef struct _Node{
    char data;
    struct _Node *lchild;
    struct _Node *rchild;
} Node,*Tree;

/* 生成二叉树的普通方法
* 按先序次序输入二叉树中结点的值
* 构造二叉链表表示的二叉树T。输入空格表示空子树。 */
Node * CreateTree()
{
    char ch;
    scanf("%c",&ch);
    Node *T;

    if(ch==' ') /* 空 */
        return NULL;
    else
    {
        T=(Node *)malloc(sizeof(Node));
        if(!T)
            exit(0);
        T->data=ch; /* 生成根结点 */
        T->lchild = CreateTree(); /* 构造左子树 */
        T->rchild = CreateTree(); /* 构造右子树 */
    }
    return T;
}
/* 由先根序列和中根序列生成二叉树
* 递归法。pre 是先跟序列，in是中根序列
* pre_s是先根序列的起始，pre_e是先跟序列的结束
* in_s是中根序列的起始,in_e是中根序列的结束
*/
Node *Convert(char pre[], int pre_s, int pre_e,
              char in [], int in_s , int in_e )
{
    if(in_s > in_e)return NULL;

    int i = in_s;
    for(i=in_s;i<in_e&&in[i]!=pre[pre_s];i++);

    Node *p = (Node *)malloc(sizeof(Node));
    p->data = pre[pre_s];
    p->lchild = Convert(pre, pre_s+1, pre_s+i-in_s,
                        in, in_s,i-1);
    p->rchild = Convert(pre, pre_s+i-in_s+1,pre_e,
                        in, i+1,in_e);

    return p;
}
/*求二叉树的度*/
int GetDegree(const Tree head)
{
    int degree = 0;
    int m,n;
    if(!head)return 0;

    if(head->lchild && head->rchild) return 2;
    else if(!head->lchild && !head->rchild) return 0;
    else {
        m = GetDegree(head->lchild) ;
        n = GetDegree(head->rchild) ;
        if(2==m || 2==n)return 2;
        else return 1;
    }
    return degree;
}
/*求二叉树的高度*/
int GetHight(const Tree head)
{
    int m,n;

    if(!head)return 0;

    m = GetHight(head->lchild);
    n = GetHight(head->rchild);

    return 1 + (m > n ? m : n);

}
/* 输出二叉树中某个指定元素的祖父节点(包括自己)
* 递归思想：如果此节点在其子树中，那么它是祖父节点
* 返回值：1表示子树中有，0表示无*/
int GetGrandPa(const Tree head, const char e)
{
   if(!head)return 0;

   if(GetGrandPa(head->lchild,e) || GetGrandPa(head->rchild,e) || e==head->data)//子树中有此节点
   {
       printf("%c",head->data);
       return 1;
   }
   else return 0;
}
/*遍历二叉树，参数oder控制遍历方式*/
void Tranverse(Node *head,int oder)
{
    if(!head)return ;
    if(LEVEL_ODER == oder)
    {
        LevTranverse(&head,1);
        return;
    }

    if(PRE_ODER == oder) printf("%c\t",head->data);
    Tranverse(head->lchild,oder);
    if(IN_ODER == oder) printf("%c\t",head->data);
    Tranverse(head->rchild,oder);
    if(BACK_ODER == oder) printf("%c\t",head->data);
    return;
}
/* 层次化遍历，采用递归思想而不用队列。
* 递归思想：把当前层遍历的同时把下一层存储好
* nodes[]存储的当前层的节点，count表示当前层的元素个数*/
void LevTranverse(const Node* nodes[], int count)
{
    int i=0, j=0;

    if(0 == count) return;

    Node *nextNodes[100] = {0};
    for(i = 0,j=0; i<count; i++)
    {
        printf("%c\t",nodes[i]->data);
        if(nodes[i]->lchild)nextNodes[j++] = nodes[i]->lchild;
        if(nodes[i]->rchild)nextNodes[j++] = nodes[i]->rchild;
    }
    LevTranverse(nextNodes,j);
    return;
}

int main(int argc, char *argv[])
{   www.zzzyk.com
    char pre[]= "abcde";
    char in[] = "bcade";
    Node *head = NULL;

    head = Convert(pre,0,strlen(pre)-1,
                   in ,0,strlen(in)-1);

    printf("Hight : %d\n",GetHight(head));
    printf("Degree : %d\n",GetDegree(head));
    if(!GetGrandPa(head,'c'))printf("No grandpa !");printf("\n");
    Tranverse(head,LEVEL_ODER);printf("\n");

    system("PAUSE");
}

补充：软件开发 , C++ ,