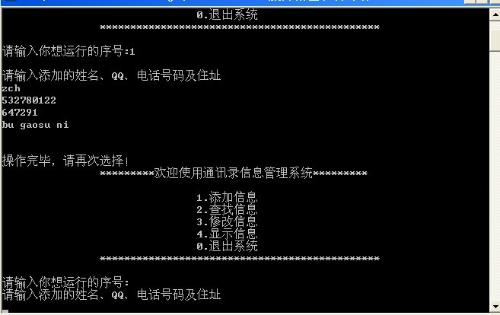
分治--大数相乘

题目：大数相乘，例如:a=423405293459和b=323452345234533相乘a*b。

这里我们采用分治的思想：

1：将该问题分成b的每个数和a相乘。

2：将每个数和a相乘得到结果存入一个数组中，每个数对应一个数组。

3：合并每个数组，相加。。

#include<iostream>  
#include<string>  
using namespace std;  
  
void main()  
{  
    string a="423405293459";  
    string b="323452345234533";  
      
    int length_a=a.length();  
    int length_b=b.length();  
    int offset=-1;  
    char* data=new char[length_b*(length_a+length_b)];//记录每个b的元素值乘以a的每个元素的二维数组（可以这么理解）  
    memset(data,'0',length_b*(length_a+length_b));  
    int count;  
    int i;  
    int j;  
    int flag;  
    for(i=length_b-1;i>=0;i--)  
    {  
        offset++;//因为每次b乘以a的起始位置都要往左偏移一位，记录当前应该偏移多少位  
        count=-1;//记录当前乘以a元素的位置  
        flag=0;  
        for(j=length_a-1;j>=0;j--)  
        {  
            count++;  
            data[(length_b-1-i)*(length_a+length_b)+(length_a+length_b-1)-offset-count]=((b[i]-'0')*(a[j]-'0')+flag)%10+'0';  
            flag=((b[i]-'0')*(a[j]-'0')+flag)/10;  
        }  
        count++;  
        data[(length_b-1-i)*(length_a+length_b)+(length_a+length_b-1)-offset-count]=flag+'0';//保证本次相乘的最后的进位也要存进去  
        for(int m=0;m<length_a+length_b;m++)  
            cout<<data[(length_b-1-i)*(length_a+length_b)+m]<<" ";//测试用的,方便我们观察  
        cout<<endl;  
    }  
    char* temp=new  char[length_a+length_b+1];  
    temp[length_a+length_b]=0;  
    memset(temp,'0',length_a+length_b);  
    int index=length_a+length_b-1;  
    flag=0;  
    int num;  
    for(i=(length_a+length_b-1);i>=0;i--)  
    {  
        num=0;  
        for(j=0;j<length_b;j++)  
        {  
            num+=(data[j*(length_a+length_b)+i]-'0');  
        }  
        num+=flag;  
        temp[index--]=num%10+'0';  
        flag=num/10;  
    }  
    char* result=temp;  
    while(*result=='0')  
        result++;  
    cout<<result<<endl;  
}

补充：软件开发 , C++ ,