谈谈 Hash Table

一.数据结构

在我们编程的世界里数据的基本组织可以说有三种形式。

1. 结构体(或对象)
2. 数组
3. 链表

其他任何的数据组织形式都可以看作是这三种数据组织形式的组合变体。

结构体(或对象)可以是基本数据类型或者其他结构体(或对象)的组合。结构体或对象一般用来描述一个复杂数据实体。

数组一般是一组同类型的变量的集合，在内存中表现为一片连续的空间，因为空间是连续的，且每一个数据单元占的内存空间的大小是相等的，所以可以根据地址的偏移对数据元素实现快速访问，但是当需要插入或者删除一个元素的时候，则需要对目标元素的之后的所有元素进行移动了。

链表的单个节点一般为结构体或者对象，因为链表的单个节点除了需要保存数据之外还需要维护它的相邻节点的关系，如果想获得链表中的某个节点的值，需要从链表的头结点开始遍历，直到找到需要的东西，而插入或者删除某个节点的话，需要找到相应的节点，修改其以及其相邻节点的相关指针的引用即可。

像其他的数据结构，比如 队列，栈，树，都可以通过数组或者链表来组织，并实现相应的操作功能。

二.Hash Table

这个世界上没有十全十美的东西，所以我们要学会取舍。任何技术的实现都没有最好的只要最合适的，也就说实现的最佳方案是和应用场景息息相关的。
很多时候，我们想对数据进行快速的存取（比如缓存的实现），并用一个key来标记自己存取的数据。我们可以把它叫做key-value的结构。
说到“快速”我们很快想到数组，因为数组可以在O(1)的时间复杂内完成指定位置元素的读写操作。
所以在理想状态，如果一个数组足够长，且存在一个函数可以将每一个key映射到唯一的一个数组下标，那么我们就可以很完美的解决问题。但往往资源都是有限的，我们没有那么大的空间，也不能设计一个无比负责的映射算法保证每一个key对应到一个唯一的数组下标。所以我们会选择一些折中的方案。

hash table便是为解决这类问题而存在的。

1.哈希函数

Hash或者你可以翻译成散列或者杂凑，hash操作其本质上就是将一个数据映射成另一个数据，通常情况下原数据的长度比hash后的数据容量大。
这种映射的关系我们叫做哈希函数。

一般情况下 哈希函数的输入可能的总数要远远多于哈希值所能表示的总数，所以就有可能两个不同的输入对应同一个哈希值，通常把具有不同关键码而具有相同哈希值的记录称作“同义词”。
在信息安全领域中也经常使用到哈希函数，不过需要使用的是单向哈希函数，就是无法通过哈希的结果反推出输入，所以经常应用于密码的加密，传输内容的完整性检查，在安全领域常用的哈希算法有 MD5，SHA1等。
在哈希表的应用中，哈希函数常用余数法进行，也就是通过求模的方式算出哈希值。

2.哈希表

哈希表是一种数据结构，实现key-value的快速存取。之前说过数组可以实现快速存取，所以哈希表肯定会使用到数组。在这里，我们把每一个数组的单元叫做一个bucket（桶）。

构造哈希函数

这里哈希函数的作用就是将key映射到一个存储地址。所以构造一个哈希表我们得先构造哈希函数。
如果一个key哈希后对应地址中已经存放了值了，这种情况我们叫做哈希冲突（Hash collisions）。
如果存在一个哈希函数，使得每一个输入都能对应到唯一的一个存储单元中（没有冲突），那么这样的哈希函数我们可以叫它完美哈希函数（Perfect Hash Function，简称PHF)。
但为了哈希函数简单，运行速度快，往往不会使用完美哈希函数。所以冲突肯定会存在的，为了减少冲突，我们希望哈希函数的结果均匀的分布在地址单元的空间中。这样可以有效的减少冲突。

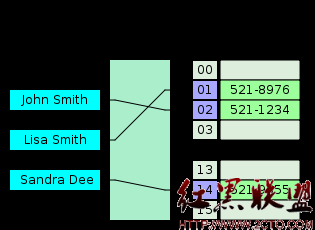
装填因子Load factor a=哈希表的实际元素数目(n)/ 哈希表的容量(m) a越大，哈希表冲突的概率越大，但是a越接近0，那么哈希表的空间就越浪费。
一般情况下建议Load factor的值为0-0.7，Java实现的HashMap默认的Load factor的值为0.75，当装载因子大于这个值的时候，HashMap会对数组进行扩张至原来两倍大。

冲突解决

既然冲突不可避免，那么我们就必须对冲突进行解决(总不能把之前的内容覆盖掉把),
解决冲突的方式主要分两类
开放定址法(Open addressing)这种方法就是在计算一个key的哈希的时候，发现目标地址已经有值了，即发生冲突了，这个时候通过相应的函数在此地址后面的地址去找，直到没有冲突为止。这个方法常用的有线性探测，二次探测，再哈希。
这种解决方法有个不好的地方就是，当发生冲突之后，会在之后的地址空间中找一个放进去，这样就有可能后来出现一个key哈希出来的结果也正好是它放进去的这个地址空间，这样就会出现非同义词的两个key发生冲突。


链接法(Separate chaining)链接法是通过数组和链表组合而成的。当发生冲突的时候只要将其加到对应的链表中即可。

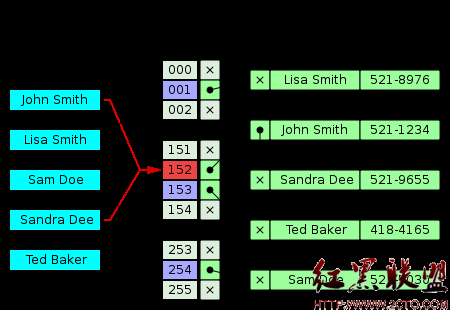
与开放定址法相比，链接法有如下几个优点：
①链接法处理冲突简单，且无堆积现象，即非同义词决不会发生冲突，因此平均查找长度较短；
②由于链接法中各链表上的结点空间是动态申请的，故它更适合于造表前无法确定表长的情况；
③开放定址法为减少冲突，要求装填因子α较小，故当结点规模较大时会浪费很多空间。而链接法中可取α≥1，且结点较大时，拉链法中增加的指针域可忽略不计，因此节省空间；
④在用链接法构造的散列表中，删除结点的操作易于实现。只要简单地删去链表上相应的结点即可。而对开放地址法构造的散列表，删除结点不能简单地将被删结点的空间置为空，否则将截断在它之后填人散列表的同义词结点的查找路径。这是因为各种开放地址法中，空地址单元(即开放地址)都是查找失败的条件。因此在 用开放地址法处理冲突的散列表上执行删除操作，只能在被删结点上做删除标记，而不能真正删除结点。

当然链接法也有其缺点，拉链法的缺点是：指针需要额外的空间，故当结点规模较小时，开放定址法较为节省空间，而若将节省的指针空间用来扩大散列表的规模，可使装填因子变小，这又减少了开放定址法中的冲突，从而提高平均查找速度

补充：综合编程 , 其他综合 ,

上一个：bat中处理字符串的方法
下一个：cocos2d-x初探学习笔记（20）--物理引擎box2d(2)