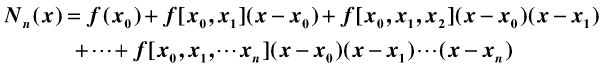[算法分析]插值法:拉格朗日插值、牛顿插值
拉格朗日插值法
(*以下定义选自易做图)
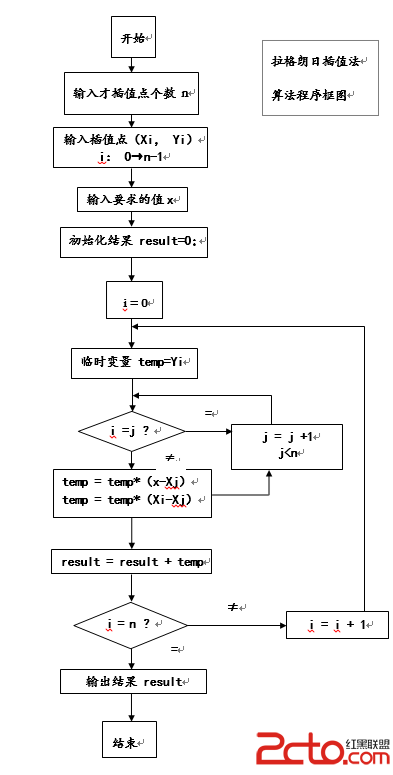
算法流程图
算法代码
[cpp]
#include<iostream>
#include<string>
#include<vector>
using namespace std;
double Lagrange(int N,vector<double>&X,vector<double>&Y,double x);
int main(){
char a='n';
do{
cout<<"请输入差值次数n的值:"<<endl;
int N;
cin>>N;
vector<double>X(N,0);
vector<double>Y(N,0);
cout<<"请输入插值点对应的值及函数值(Xi,Yi):"<<endl;
for(int a=0;a<N;a++){
cin>>X[a]>>Y[a];
}
cout<<"请输入要求值x的值:"<<endl;
double x;
cin>>x;
double result=Lagrange(N,X,Y,x);
cout<<"由拉格朗日插值法得出结果: "<<result<<endl;
cout<<"是否要继续?(y/n):";
cin>>a;
}while(a=='y');
return 0;
}
double Lagrange(int N,vector<double>&X,vector<double>&Y,double x){
double result=0;
for(int i=0;i<N;i++){
double temp=Y[i];
for(int j=0;j<N;j++){
if(i!=j){
temp = temp*(x-X[j]);
temp = temp/(X[i]-X[j]);
}
}
result += temp;
}
return result;
};
牛顿插值法
牛顿插值法公式如下,具体参见(百度文档)
算法流程
算法代码
[cpp]
#include<iostream>
#include<string>
#include<vector>
using namespace std;
double ChaShang(int n,vector<double>&X,vector<double>&Y);
double Newton(double x,vector<double>&X,vector<double>&Y);
int main(){
int n;
cin>>n;
vector<double>X(n,0);
vector<double>Y(n,0);
for(int i=0;i<n;i++){
cin>>X[i]>>Y[i];
}
double x;
cin>>x;
cout<<Newton(x,X,Y);
}
double ChaShang(int n,vector<double>&X,vector<double>&Y){
double f=0;
double temp=0;
for(int i=0;i<n+1;i++){
temp=Y[i];
for(int j=0;j<n+1;j++)
if(i!=j) temp /= (X[i]-X[j]);
f += temp;
}
return f;
}
double Newton(double x,vector<double>&X,vector<double> &Y){
double result=0;
for(int i=0;i<X.size();i++){
double temp=1;
double f=ChaShang(i,X,Y);
for(int j=0;j<i;j++){
temp = temp*(x-X[j]);
}
result += f*temp;
}
return result;
}
实验过程原始记录
给定函数四个点的数据如下:
试用拉格朗日插值确定函数在x=2.101,4.234处的函数值。
运行得到结果:
已知用牛顿插值公式求的近似值。
运行程序得到结果: 2.26667
实验分析
1、Lagrange插值法和Newton插值法解决实际问题中关于只提供复杂的离散数据的函数求值问题,通过将所考察的函数简单化,构造关于离散数据实际函数f(x)的近似函数P(x),从而可以计算未知点出的函数值,是插值法的基本思路。
2、实际上Lagrange插值法和Newton插值法是同一种方法的两种变形,其构造拟合函数的思路是相同的,而实验中两个实际问题用两种算法计算出结果是相同的。
3、实验所得结果精确度并不高,一方面是因为所给数据较少,另一方面也是主要方面在Win32中C++中数据类型double精度只有7位,计算机在进行浮点运算时截断运算会导致误差。实际问题中,测量数据也可能导致误差。
4、在解决实际问题中,更多是利用精确且高效的计算机求解。所以解决问题时不仅要构造可求解的算法,更重要是构造合理的可以编写成程序由计算机求解的算法,而算法的优化不仅可以节省时间空间,更能得到更为精确有价值的结果。
补充:软件开发 , C++ ,