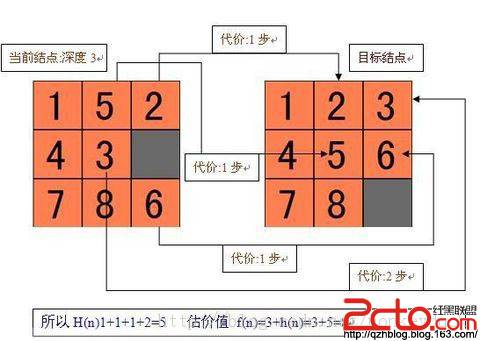
图的着色问题 (也就是最少着色问题,时间复杂度为N^2)
问题起源于一个宣讲会时间安排问题,有若干个部门要进行宣讲会,有若干个同学对多个部门有兴趣,希望在给出一个时间方案,要求所有的同学都可以参加所有他感兴趣的宣讲会,同时要求在最短的时间内把宣讲会结束。
把每个宣讲会作为一个点,每个同学感兴趣的宣讲会两两相连,就变成了一个图的最少着色问题。
而图的着色问题可以在多项式时间内完成(为什么有的书上说没有多项式算法?感觉很奇怪,明明可以做到),图的颜色编号,也就是宣讲会的宣讲时间编号,其中最大的颜色编号也就是所需要的最长时间 。
算法思想: 深度遍历,遍历过程中设置顶点的颜色,设定规则是: 查找所有相邻的顶点,选择一个未被使用过的编号最小的颜色,把这个颜色作为当前节点颜色。
算易做图确性: 算法执行过程,保证了每个顶点都与其他相邻顶点颜色不同,同时又保证了使用最少的颜色数目,显然是正确的。
#include <iostream>
#define Max 15
using namespace std;
int vertexCount=0;
int color[Max]={0};
int arc[Max][Max]={0};
int visited[Max]={0};
void init()
{
cout<<"请输入定点数目:\n";
cin>>vertexCount;
int t;
cout<<"请输入边的数目:\n";
cin>>t;
for(int i=0;i!=t;++i)
{
cout<<"请输入第"<<i+1<<"条边:\n";
int a,b;
cin>>a>>b;
arc[a-1][b-1]=1;
arc[b-1][a-1]=1;
}
}
void DFSTraverse(int s)
{
if(visited[s]) return;
int t=1;
bool flag;
do{
flag=false;
for(int i=0;i!=vertexCount;++i)
{
if(arc[s][i]&&color[i]==t)
{
flag=true;
t++;
break;
}
}
}while(flag);
color[s]=t;
visited[s]=1;
for(int i=0;i!=vertexCount;++i)
{
if(arc[s][i]&&visited[i]==0)
DFSTraverse(i);
}
}
void show()
{
for(int i=0;i!=vertexCount;++i)
cout<<"顶点"<<i+1<<" 颜色"<<color[i]<<endl;
}
void main()
{
init();
for(int i=0;i!=vertexCount;++i)
DFSTraverse(i);
show();
::system("pause");
}
补充:软件开发 , C++ ,