hdu 4491 Windmill Animation（几何+模拟）

 

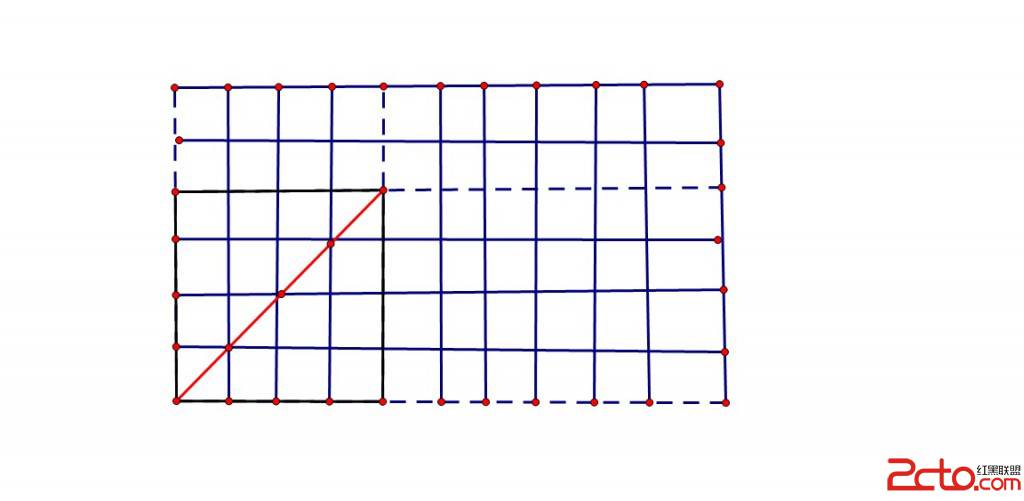
考虑到n很小，可以模拟来搞。每次得到一个原点及斜率，然后构造出在直线上原点(O)的上方(rp）和下方(rn)两个点。然后依次每个不在该直线上的点，如果该点在直线上方，那么要达到该点逆时针旋转的角度为向量 rp->O 和向量 p->O的夹角。反之则是向量O->rp和向量O->rn的夹角。

 

 

 

#include<algorithm>  
#include<iostream>  
#include<cstring>  
#include<fstream>  
#include<sstream>  
#include<cstdlib>  
#include<vector>  
#include<string>  
#include<cstdio>  
#include<bitset>  
#include<queue>  
#include<stack>  
#include<cmath>  
#include<map>  
#include<set>  
#define FF(i, a, b) for(int i=a; i<b; i++)  
#define FD(i, a, b) for(int i=a; i>=b; i--)  
#define REP(i, n) for(int i=0; i<n; i++)  
#define CLR(a, b) memset(a, b, sizeof(a))  
#define debug puts("**debug**")  
#define LL long long  
#define PB push_back  
#define MP make_pair  
using namespace std;  
  
const double eps = 1e-8;  
const double PI = acos(-1.0);  
int dcmp(double x) {  
  if(fabs(x) < eps) return 0; else return x < 0 ? -1 : 1;  
}  
  
struct Point {  
  double x, y;  
  Point(double x=0, double y=0):x(x),y(y) { }  
};  
  
typedef Point Vector;  
  
Vector operator + (Vector A, Vector B) { return Vector(A.x+B.x, A.y+B.y); }  
Vector operator - (Point A, Point B) { return Vector(A.x-B.x, A.y-B.y); }  
Vector operator * (Vector A, double p) { return Vector(A.x*p, A.y*p); }  
Vector operator / (Vector A, double p) { return Vector(A.x/p, A.y/p); }  
  
bool operator < (const Point& a, const Point& b) {  
  return a.x < b.x || (a.x == b.x && a.y < b.y);  
}  
  
bool operator == (const Point& a, const Point &b) {  
  return dcmp(a.x-b.x) == 0 && dcmp(a.y-b.y) == 0;  
}  
  
double Dot(Vector A, Vector B) { return A.x*B.x + A.y*B.y; }  
double Length(Vector A) { return sqrt(Dot(A, A)); }  
double Angle(Vector A, Vector B) { return acos(Dot(A, B) / Length(A) / Length(B)); }  
double angle(Vector v) { return atan2(v.y, v.x); }  
double torad(double ang)  
{  
    return ang / 180 * PI;  
}  
  
void getLineGeneralEquation(const Point& p1, const Point& p2, double& a, double& b, double &c) {  
  a = p2.y-p1.y;  
  b = p1.x-p2.x;  
  c = -a*p1.x - b*p1.y;  
}  
  
Point read_point()  
{  
    Point a;  
    scanf("%lf%lf", &a.x, &a.y);  
    return a;  
}  
  
const int maxn = 30;  
int P, cas, ind, n, s, st, ans[maxn];  
double ang;  
Point p[maxn];  
  
int main()  
{  
    scanf("%d", &P);  
    while(P--)  
    {  
        scanf("%d%d%d%d%lf", &cas, &n, &s, &st, &ang);  
        ang = torad(ang);  
        FF(i, 1, n+1)  
        {  
            scanf("%d", &ind);  
            p[ind] = read_point();  
        }  
        int tot = 0, id1 = st, id2 = st;  
        Point now = p[st];  
        while(tot < s)  
        {  
            int nxt;  
            double a, b, c, tmp, tang, nxtang = 1e50;  
            Point O = now, rp = O + Point(1000*cos(ang), 1000*sin(ang)) , rn = O - Point(1000*cos(ang), 1000*sin(ang));  
            getLineGeneralEquation(O, rp, a, b, c);  
            FF(i, 1, n+1) if(i != id1 && i != id2)  
            {  
                tmp = a*p[i].x + b*p[i].y + c;  
                if(tmp > 0) tang = Angle(rn-O, p[i]-O);  
                else if(tmp < 0) tang = Angle(rp-O, p[i]-O);  
                else tang = 0;  
                if(dcmp(nxtang - tang) > 0) nxtang = tang, nxt = i;  
            }  
            ans[tot++] = nxt;  
            ang = angle(now-p[nxt]);  
            now = p[nxt];  
            id1 = id2;  
            id2 = nxt;  
        }  
        printf("%d", cas);  
        REP(i, tot) printf(" %d", ans[i]);  
        puts("");  
    }  
    return 0;  
}  

 

补充：软件开发 , C++ ,